具志川職業能力開発校、浦添職業能力開発校 共通
直線y=x+1 ・・・・① のグラフはx軸、y軸とそれぞれ2点A、Bで交わり、①上のy座標が3である点Eにおいて傾きが-1/2の直線②と交わる。また、②のグラフとx軸、y軸との交点はそれぞれ点C、Dであるとする。次の問に答えなさい。
[問題1] 直線②の式を求めなさい。
[問題2] 四角形EBACの面積を求めなさい
解答と解説
試験問題1の解答:y=-x/2+4
まずは、実際にグラフを描いた方が間違える可能性が低くなります。
y=x+1
のグラフは、y軸の切片が1、傾きが1の直線グラフだと分かります。グラフにすると下図の通りです。
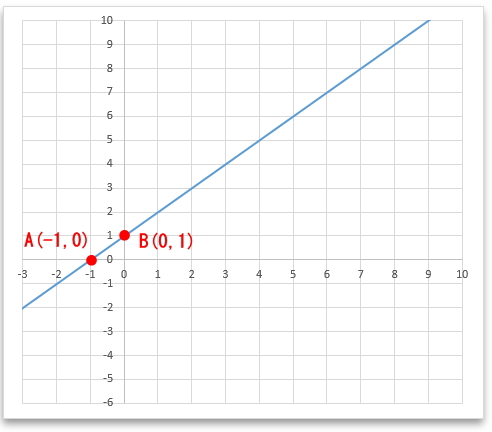
さらにこの直線①のy座標が3である点で傾き-1/2の直線②と交わるということなので、直線②のグラフ式は次の通り。
直線①のy座標が3である点Eを通るということなので、点Eは、直線①の式にy=3を代入すればx座標が求まります。
y=x+1
3=x+1
x=3-1
x=2
よって、点Eの座標はE(2、3)。更に傾きが-1/2のグラフだと分かっているので、直線式にこれらの分かっている値を代入すると、直線②の式が求まります。
y=ax+b
傾きが-1/2なので、a=-1/2だとわかります。
y=-x/2+b
更に点E(2、3)を通るので、上の式に代入すると切片bが求まります。
3=-2/2+b
3=-1+b
b=4
よって、直線②の式は、
y=-x/2+4
試験問題2の解答:16.5
直線①と②グラフ式は、問題1でy=-x/2+4と分かりました。図は下図の通り。
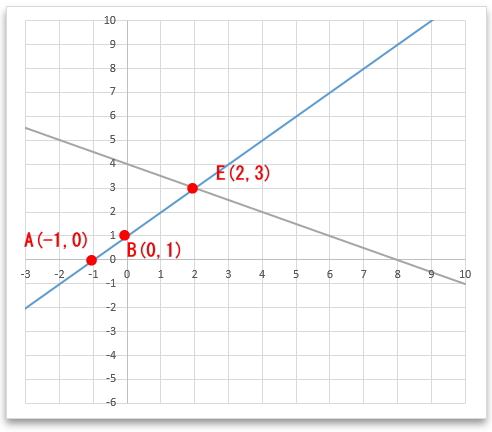
直線②のx座標とy座標の交点が点C、Dということなので、点CとDの座標は次の通り。
点Cの座標
y=0を式②へ代入
y=-x/2+4
0=-x/2+4
x/2=4
x=8
よって、点Cの座標は(8, 0)
点Dの座標
x=0を式②へ代入
y=-x/2+4
y=-0+4
y=4
よって、点Dの座標は(0, 4)
グラフ図にすると下図の通り。
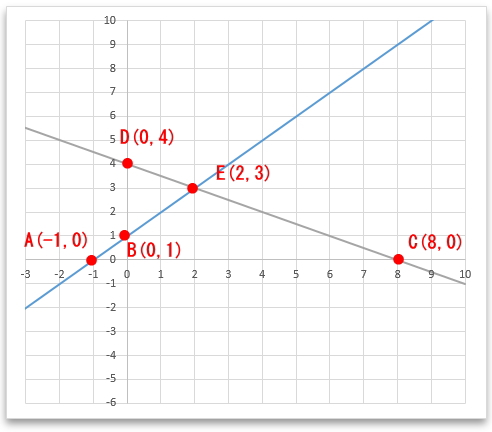
そして、四角形DBACは次の通り。
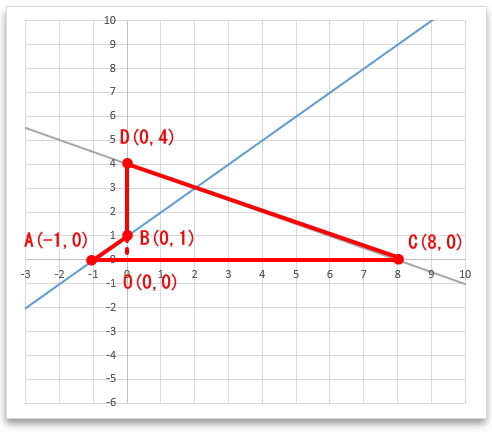
四角形DBACの面積を求めるには、まずは、原点をOとした場合、三角形DOCの面積を求め、更に三角形ABOを足すことで求められます。
三角形DOCの面積
点Dから原点Oのy座標の距離4が、三角形の高さとなります。
更に原点Oから点CのX座標の距離8が三角形の底辺の長さとなります。よって、三角形DOCの面積は
三角形DOCの面積=8×4÷2=16
三角形ABOの面積
点Bから原点Oのy座標の距離1が、三角形の高さとなります。
更に原点Oから点AのX座標の距離1が三角形の底辺の長さとなります。よって、三角形ABOの面積は
三角形ABOの面積=1×1÷2=0.5
よって、四角形DBACの面積は
四角形DBACの面積=16+0.5=16.5
※解説の内容が不明、不十分というのがあればコメントをください。

