平成27年2月20日に大阪で実施された職業訓練の選考試験問題と解説です。大阪で行われる職業訓練の試験問題は、筆記試験ではなく毎回、選択方式です。問題傾向も毎回同じなのでこれらの過去問を繰り返し実施し、短時間かつ正確に解けるようにしておきましょう。
次の方程式を解き、適当な数字を次のア~オの中から選び、答えなさい。
[問題1] 3.6%の食塩水200gと5.1%の食塩水300gを混ぜ合わせると、何%の食塩水ができるか。
312
ア 4.1% イ 4.2% ウ 4.3% エ 4.4% オ 4.5%
[問題2] 現在、兄と弟は6歳差です。ちょうど5年後、この兄と弟の年齢の比が9:7になる。現在の兄の年齢を求めなさい。
ア 13歳 イ 19歳 ウ 22歳 エ 28歳 オ 31歳
[問題3] ある商品は定価では売れなかったので、定価の2割引で売ったところ、それでも仕入れ値の2割の利益があった。定価が3600円であるとき、仕入れ値を求めなさい。
ア 2400円 イ 2500円 ウ 2600円 エ 2700円 オ 2800円
[問題4] 中心角90°面積が5πのおうぎ形と、中心角120°面積が15πのおうぎ形の半径を比べると何倍であるか求めよ。
ア 1.3倍 イ 1.4倍 ウ 1.5倍 エ 1.6倍 オ 1.7倍
[問題5] 縦の長さが240cm、横の長さが312cmである長方形の紙を、余ることなく同じ大きさの正方形に切り分ける。正方形の大きさを最大にするとき、何枚の正方形ができるか求めよ。
ア 120枚 イ 125枚 ウ 130枚 エ 135枚 オ 140枚
解答と解説
試験問題1の解答:オ
食塩水の濃度を求める公式を頭に入れておく必要があります。
食塩水の濃度(%)=食塩の量 ÷ 食塩水の量
3.6%の食塩水200gに含まれる食塩の量を求める
公式より
食塩水の濃度(%)=食塩の量 ÷ 食塩水の量
3.6%=食塩の量 ÷ 200g
0.036=食塩の量 ÷ 200
食塩の量=0.036 × 200
=7.2g
5.1%の食塩水300gに含まれる食塩の量を求める
公式より
食塩水の濃度(%)=食塩の量 ÷ 食塩水の量
5.1%=食塩の量 ÷ 300g
0.051=食塩の量 ÷ 300
食塩の量=0.051 × 300
=15.3g
3.6%の食塩水200gと5.1%の食塩水300gの混合食塩水
3.6%の食塩水200gと5.1%の食塩水300gの食塩水を混ぜると、
食塩水の量=200g+300g=500g
更に食塩の量は、3.6%の食塩水200gに含まれる食塩の量は、7.2g。3.6%の食塩水200gに含まれる食塩の量は、15.3gなので、混合食塩水に含まれる食塩の量は、
食塩の量=7.2g+15.3g=22.5g
よって、混合食塩水の濃度は、公式より
食塩水の濃度(%)=食塩の量 ÷ 食塩水の量
食塩水の濃度(%)=22.5 ÷ 500
=0.045
=4.5%
試験問題2の解答:ウ
『兄と弟の年齢の比が9:7』という表現に惑わされてはだめ。これは、兄の年齢が弟の年齢の9/7倍ということ。兄が9歳、弟が7歳として考えると9/7倍というのはすぐに分かる。
求めたい兄の現在の年齢をXとした場合、弟とは6歳差なので各々の年齢は次のように表すことができます。
兄の年齢=X
弟の年齢=X-6
そして、5年後の年齢は共に5歳年を取るので、各々の年齢は次のように表すことができます。
兄の年齢=X+5
弟の年齢=X-6+5=X-1
また、このとき兄の年齢は弟の年齢の9/7倍になるので次の式が成り立ちます。
兄の年齢=弟の年齢×9/7
(X+5)=(X-1)×9/7
この式を解けば求めたい兄の現在の年齢Xが出てきます。
(X+5)=(X-1)×9/7
(X+5)×7=(X-1)×9
7X+35=9X-9
-2X=-44
X=22
よって、兄の現在の年齢は22歳
試験問題3の解答:ア
求めたい仕入れ値をXと仮定します。
最終的に割引きしても仕入れ値の2割の利益があったということなので、その利益額は次の式で表すことができます。
利益額=仕入れ値 × 2割
=X × 0.2
=0.2X
利益額が0.2Xと分かりました。よって、実際に売った値段は、仕入れ値にこの利益額0.2Xを上乗せした額だと分かります。よって、その売値は
売値=仕入れ値+利益額
=X+0.2X
=1.2X ・・・(1)
また、売値を別の角度から求めます。定価3600円の2割引きで売ったということなので、売値は次の通りになります。
売値=定価-(定価×割引き率)
=3600-(3600×0.2)
=2880
定価の2割引きということは、定価の8割で売るということなので、
売値=定価×0.8
=3600×0.8
=2880
として求めてもよい。
この売値2880円が(1)と同じになるはずなので、次の式が成り立ちます。
1.2X=2880
この式を解くと求めたい仕入れ値Xが出てきます。
1.2X=2880
X=2400
よって、仕入れ値は2400円
試験問題4の解答:ウ
ここで使用するのは、円の面積を求める公式です。
円の面積=半径×半径×Π
中心角90°、面積が5πのおうぎ形の半径を求める
求めたい半径をRとします。中心角が90°ということは、半径Rの円を1/4(90÷360)にした円になります。下図の赤線のような扇形ですね。
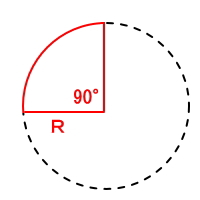
よって、この扇形の面積は半径Rの面積を1/4したものと同じになります。
半径Rの円の面積は、公式より
半径Rの面積=R×R×Π
=R²Π
扇形の面積はこの円の面積の1/4なので次の通り。
扇形の面積=半径Rの面積×1/4
=R²Π/4
また、この扇形の面積が5Πということなので次の式が成り立ちます。
5Π=R²Π/4
この式を解くと半径Rが求まります。
5Π=R²Π/4
20Π=R²Π
R²=20
R=√20
R=√2²×5
R=2√5
中心角 120°、面積が15πのおうぎ形の半径を求める
求めたい半径をrとします。中心角が120°ということは、半径rの円を1/3(120÷360)にした円になります。よって、この扇形の面積は半径rの面積を1/3したものと同じになります。
半径rの円の面積は、公式より
半径rの面積=r×r×Π
=r²Π
扇形の面積はこの円の面積の1/3なので次の通り。
扇形の面積=半径rの面積×1/3
=r²Π/3
また、この扇形の面積が15Πということなので次の式が成り立ちます。
15Π=r²Π/3
この式を解くと半径rが求まります。
15Π=r²Π/3
45Π=r²Π
r²=45
r=√45
r=√3²×5
r=3√5
2つの扇形の半径比を求める
中心角90°の扇形の半径は、
R=2√5
中心角120°の扇形の半径は、
r=3√5
と分かりました。よって、
R:r=2√5:3√5
=2:3
ようは、Rが2に対して、rが3なので1.5倍ということになります。
試験問題5の解答:ウ
イメージとしては下図のような形ですね。
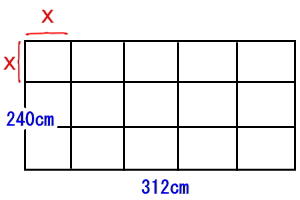
縦横が1cmの正方形の場合であれば、縦に240個、横に312個並ぶことになります。更に縦横が2cmの正方形であれば縦に120個、横に156個並ぶことになります。縦横が3cmの正方形であれば縦に80個、横に104個といったように色々な大きさの正方形を入れることができます。
これは、実は、240cmと312cmの公約数が1辺の長さとなる正方形であれば、この長方形の中に隙間なく入れることができます。
240cmと312cmの公約数は、{1、2、3、4、6、~}と複数ありますが、設問では正方形の大きさが最大となるということなので、1辺の長さが240と312の最大公約数になります。240と312の最大公約数は次の通り。
2)240 312
2)120 156
2)60 78
3)30 39
10 13
最大公約数=2×2×2×3=24
1辺が24cmの正方形だと分かりました。1辺が24cmの正方形が長方形の中に入る数は
縦に入る数=240÷24=10個
横に入る数=312÷24=13個
よって、長方形の中に入る正方形の数は、
長方形の中に入る正方形の数=10×13=130個

