大阪 職業訓練 試験問題 数学-問4(平成30年2月15日実施) 短期課程

問４ 試験問題

1 辺 24 ㎝の正方形 ABCD において、点 P は頂点 A から頂点 Bまで毎秒 3cm の速さで、点 Q は頂点 D から頂点 A まで毎秒2cm の速さで、同時に出発する。以下の問いにア～オの中から1 つ選び、記号で答えなさい。

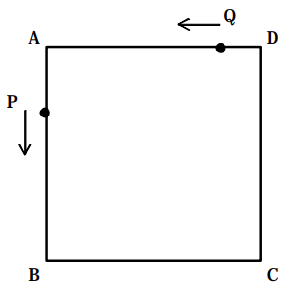
[問題1]　△CPQ の面積 S が 267cm² となるのは 2 点 P, Q が出発してから 2 回確認できた。2 回目に 267cm² になるのは何秒後か求めなさい。

[問題2]　△CPQ の面積 S の変域を求めなさい。

解答と解説

解答と解説を記載していきます。
解き方が分からないという人を少しでも減らすためにできる限り分かり易く必要以上に細かく順を追って解説している部分がありますが、実際の試験時は丁寧に計算し過ぎると時間のロスに繋がるため、自分の分かるところは効率よく解答していくようにしてください。

問題１の解答と解説

試験問題１の解答：オ

この問題を解くには距離と速度と時間の関係式を知っている必要があります。

△CPQの面積が267cm²となる時間をＴ秒後と仮定した場合、Ｔ秒後のＰとＱの移動距離は次の通りです。

距離＝速度×時間
Ｐの移動距離＝3×Ｔ＝3Ｔ
Ｑの移動距離＝2×Ｔ＝2Ｔ

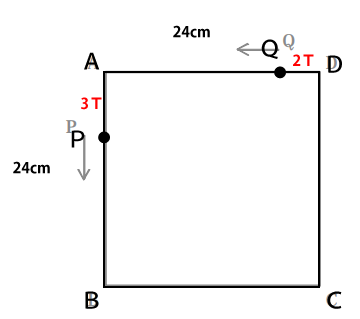
この時の△CPQの面積は次の式で表すことができます。

△CPQ＝四角形ABCD－△CBP－△PQＡ－△CDQ

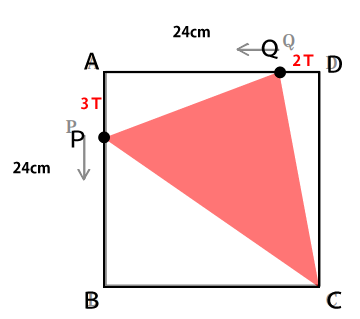
四角形ABCDの面積＝24×24＝576

PBの長さ＝24－3Ｔ
△CBPの面積＝24×(24－3Ｔ)÷2＝288－36Ｔ

APの長さ＝3Ｔ
AQの長さ＝24－2Ｔ
△PQAの面積＝3Ｔ×(24－2Ｔ)÷2＝36Ｔ－3Ｔ²

QDの長さ＝2Ｔ
△CDQの面積＝24×2Ｔ÷2＝24Ｔ

よって、△CPQの面積は次の通り

△CPQ＝四角形ABCD－△CBP－△PQＡ－△CDQ
267＝576－(288－36Ｔ)－(36Ｔ－3Ｔ²)－24Ｔ
267＝576－288＋36Ｔ－36Ｔ＋3Ｔ²－24Ｔ
267＝288＋3Ｔ²－24Ｔ
3Ｔ²－24Ｔ－21＝0
Ｔ²－8Ｔ＋7＝0
(Ｔ－7)(Ｔ－1)＝0

Ｔ＝7秒後と1秒後

2回目に267cm²になるときなので、あとの7秒後の方になる

問題２の解答と解説

試験問題２の解答：ア

△CPQ＝四角形ABCD－△CBP－△PQＡ－△CDQ
Ｓ＝576－(288－36Ｔ)－(36Ｔ－3Ｔ²)－24Ｔ
Ｓ＝576－288＋36Ｔ－36Ｔ＋3Ｔ²－24Ｔ
Ｓ＝3Ｔ²－24Ｔ＋288
　＝3(Ｔ－4)²＋240

よって、時間Ｔと面積Ｓの関係グラフは下図のような放物線になります。

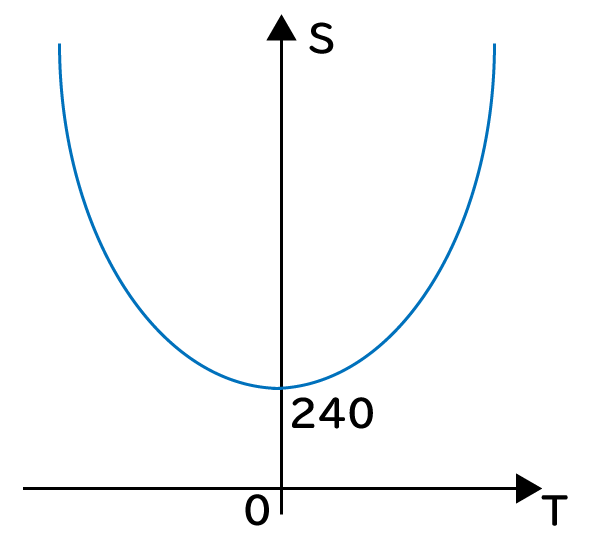
これはＴ＝0のとき、面積Ｓが最小値240になることを意味します。よって、この時点で解答はエだとわかります。

ちなみに面積Ｓの最大値はＴの時間が大きくなればなるほど大きくなるのですが、移動速度の速いＰがＢ点に到着した時点で移動がストップすると考えると、ＰがＢ点に到達するのは移動開始8秒後になります。よって、その時の面積は次の通り。

Ｓ＝3(Ｔ－4)²＋240
　＝3(8－4)²＋240
　＝3×16＋240
　＝48＋240
　＝288

よって、240≦S ≦288
　
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。