この問題は平成30年4月入校(試験実施日:平成30年2月16日)の大阪職業訓練短期過程の選考試験問題問2の解説です。特に難しい問題はありませんが、間違いやすい問題もあるのでこれらの過去問を繰り返し実施し、短時間かつ正確に解けるようにしておきましょう。
実際の試験の問題用紙は以下のページで確認することができます。
⇒大阪府職業訓練校試験問題(平成30年度2月16日実施 短期課程
問1、問3~問4に関しては以下のページに解説をまとめているので参考にして下さい。
問2 試験問題
次の文章題の答えとして正しいものをア~オの中から1つ選び、記号で答えなさい。
[問題1] 1 から 100 までの自然数の中で、6 または 7 で割り切れる数の個数を求めなさい
[解答群]
- 28個
- 29個
- 30個
- 31個
- 32個
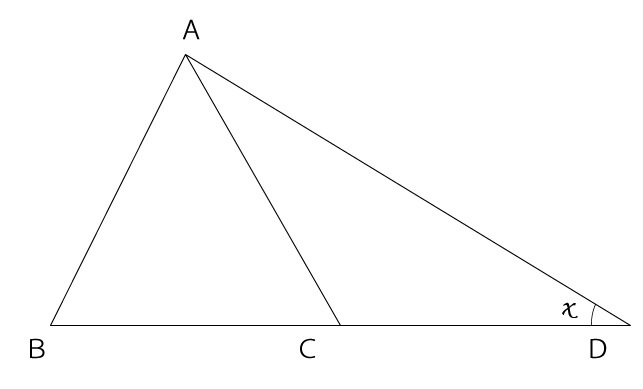
[問題2] 下の図において、AB=BC=CD=CA である。∠x の大きさを求めなさい。
[解答群]
- 25°
- 30°
- 36°
- 42°
- 45°
[問題3] ある仕事をするのに、A が 1 人でするには 12 日かかり、B が 1 人でするには 15 日かかり、C が 1 人でするには 20 日かかる。3 人で仕事をすれば何日かかるか求めなさい。
[解答群]
- 4日
- 5日
- 6日
- 7日
- 8日
[問題4] 円形の池の周りに、8m ごとに木が植えてある。木の間隔が広すぎるので 5m ごとに植え直すと 33 本余計に必要となった。池の周りの長さを求めなさい。
[解答群]
- 360m
- 400m
- 440m
- 480m
- 520m
[問題5] 姉は分速 180m の速さで西へ、妹は分速 140m の速さで東へ、同地点から同時刻に歩き出した。2 人の間の距離が 2880m となるのは歩き始めてから何分後か求めなさい。
[解答群]
- 8分後
- 9分後
- 10分後
- 11分後
- 12分後
解答と解説
解答と解説を記載していきます。
解き方が分からないという人を少しでも減らすためにできる限り分かり易く必要以上に細かく順を追って解説している部分がありますが、実際の試験時は丁寧に計算し過ぎると時間のロスに繋がるため、自分の分かるところは効率よく解答していくようにしてください。
問題1の解答と解説
試験問題1の解答:ア
1から100までの自然数の内、6で割り切れる数は次の通り。
100÷6=16.666…
16個
1から100までの自然数の内、7で割り切れる数は次の通り。
100÷7=14.285…
14個
よって、6または7で割り切れる数は16個+14個=30個あるが、重複している自然数もあるので、それを取り除く必要があります。
『重複している自然数の数』=『6と7の最小公倍数で割り切れる数』となります。
6と7の最小公倍数は、42
1から100までの自然数の内、42で割り切れる数は次の通り。
100÷42=2.38.…
2個
よって、1から100までの自然数の内、6または7で割り切れる数の個数は次の通り。
16個+14個-2個=28個
問題2の解答と解説
試験問題2の解答:イ
三角形ABCは正三角形なので、∠ACB=60°となります。よって、∠ACD=120°
また、三角形ACDは二等辺三角形なので、∠Xは次の通りになります。
∠X=(180-∠ACD)÷2=30°
問題3の解答と解説
試験問題3の解答:イ
仕事の全体量を60と仮定します。この仕事の全体量はいくつに仮定しても構わないのですが、仕事にかかる各々の日数の最小公倍数に設定すると計算が容易になります。
Aさんが一人でこの仕事すべてを行った場合、12日かかるので、1日当たりの仕事量は5になります。
同様にBさんが一人でこの仕事すべてを行った場合、15日かかるので、1日当たりの仕事量は4になります。
同様にCさんが一人でこの仕事すべてを行った場合、20日かかるので、1日当たりの仕事量は3になります。
よって、Aさん、Bさん、Cさんが3人で仕事を実施した場合、1日の仕事量は次の通りになります。
3人の1日の仕事量=5+4+3=12
よって、3人で仕事を実施した場合、仕事を終えるのにかかる日数は次の通りになります。
仕事を終えるのにかかる日数=60÷12=5日
問題4の解答と解説
試験問題4の解答:ウ
求めたい池の周りの長さをNと仮定します。また、8m間隔で木を植えたさいの本数をMとすると次の式が成り立ちます。
N=8×M
=8M・・・①
また、気の間隔を5mすると、33本余計に必要になったということなので次の式が成り立ちます。
N=5×(M+33)
=5M+165・・・②
式①②より、
8M=5M+165
3M=165
M=55
これを式①へ代入します。
N=8×55
=440
よって、池の周りの長さは440m
問題5の解答と解説
試験問題5の解答:イ
この問題を解くには、速度と距離と時間の関係式をしている必要があります。

二人が歩き始めてから両者の距離が2880mとなる時間をHと仮定すると下記の式が成り立ちます。
姉の移動距離=速度×時間
=180×H
=180H
妹の移動距離=速度×時間
=140×H
=140H
この二人の移動距離の合計が2880mとなるので次の式が成り立ちます。
180H+140H=2880
320H=2880
H=9
よって、二人の距離が2,880mとなるのは9分後
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

