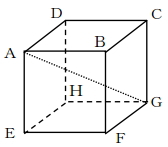
(８) 図のような立方体で、対角線ＡＧの長さを9cmとしたとき、次の各問に答えなさい。
[問題１]
ＡＥの長さを求めなさい。
[問題２]
立方体の体積を求めなさい。
解答と解説
問題１の解説：
この問題を解くには、立方体とはどういった図形なのか？ というのと、三平方の定理を知っておく必要があります。
立方体とは、合同な6つの正方形で囲まれた図形を立方体という。
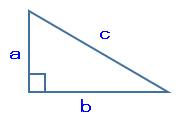
下図ような直角三角形がある場合、次の式が成り立ちます。この式を三平方の定理といいます。
a²+b²=c²
まずは、三角形ＡＥＧについて考えます。∠ＡＥＧは直角なので、上記の三平方の定理を使用することができます。三平方の定理にあてはめると次のようになります。
ＡＥ² ＋ ＥＧ² ＝ ＡＧ² ・・・(１)
次に三角形ＥＦＧについて考えます。∠ＥＦＧは直角なので、同様に三平方の定理を使用することができます。三平方の定理にあてはめると次のようになります。
ＦＧ² ＋ ＥＦ² ＝ ＥＧ² ・・・(２)
立方体は全ての辺の長さが等しいので、立方体の1辺の長さをaとした場合、式(１)(２)は式(３)(４)のようになります。
ＡＥ² ＋ ＥＧ² ＝ ＡＧ² ・・・(１)
a² ＋ ＥＧ² ＝ ＡＧ² ・・・(３)
ＦＧ² ＋ ＥＦ² ＝ ＥＧ² ・・・(２)
a² ＋ a² ＝ ＥＧ²
ＥＧ²＝2a² ・・・(４)
設問より、ＡＧは9cmと分かっているので、式(４)を式(３)へ代入することで求めたい辺ＡＥ(a)の長さを求めることができます。
a² ＋ ＥＧ² ＝ ＡＧ² ・・・(３)
a² ＋ 2a² ＝ 9²
3a² ＝ 81
a² ＝ 27
a ＝ 3√3
a ＝ ＡＥなので求めたい辺ＡＥの長さは3√3 となります。
解答：3√3 cm
問題２の解説：
立方体の体積を求める公式は、
立方体の体積 ＝ 底面積 × 高さ
底面積 ＝ (3√3) × (3√3) ＝ 9×3 ＝ 27
よって、立方体の体積は、
立方体の体積 ＝ 27 × 3√3 ＝ 81√3 cm³
解答：81√3 cm³
※解説内容に不明な点があればコメント欄にコメントください。
