埼玉 職業訓練 試験問題[長期] 数学-問3(平成23年入校生)

(７) 次の（１）～（４）の各問いに答えなさい。

[問題１]
1台6,500円で仕入れたテレビを2割のもうけを入れて売りました。売値は何円であるか求めなさい。

[問題２]
1、2、3の数字を書いた3枚のカードがある。1枚ずつ続けて3回引き、引いた順に並べて3けたの整数をつくる。3けたの整数はいくつできるか求めなさい。

[問題３]
1個10㎏の荷物1個と、1個12㎏の荷物3個と、4㎏の荷物１個がある。これらの平均の重さを求めなさい。

[問題４]
列車が一定の速度で走っている。550ｍの鉄橋を渡りはじめてから渡り終わるまで30秒かかり、また、650ｍのトンネルに入り終わってから出始めるまでに20秒かかった。列車の長さを求めなさい。

解答と解説

問題１の解説：
6,500円に2割のもうけ(利益)を入れて売るという事は、仕入れの値段6,500円に6,500円の2割の値段を上乗せした価格で売るという事。6,500円の2割の値段は、

　6500 × 0.2 ＝ 1300

よって、この1300円を仕入れの6,500円に上乗せします。

　6500 ＋ 1300 ＝ 7800

よって、求める売値は7,800円となります。

解答：7,800円

問題２の解説：
順列の公式を使います。順列の公式は次の通りです。

今回の問題であれば3種類のカードから3種類全てを選んで並べる順番の組み合わせ数なので、次のようになります。

3Ｐ3 ＝ 3×(3－1)×(3－2) ＝ 6

よって、求める組み合わせ数は6通り。

解答：6

問題３の解説：
10㎏ × 1個 ＝ 10㎏
12㎏ × 3個 ＝ 36㎏
4㎏ × 1個 ＝ 4㎏

個数の合計は、5個
重さの合計は、50㎏

1個あたりの平均の重さは

50 ÷ 5 ＝ 10

よって、平均の重さは10㎏となる。

解答：10㎏

問題４の解説：
次の公式を使用します。
速度 ＝ 距離 ÷ 時間

設問の『の鉄橋を渡りはじめてから』『渡り終わるまで』、『トンネルに入り終わってから』『出始めるまで』といった言葉に惑わされないようにしましょう。図にすると次のようになります。

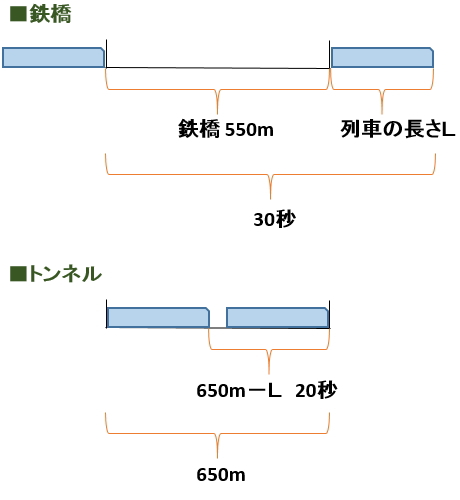
まず、鉄橋について考えます。

求めたい列車の長さをＬとした場合、鉄橋を渡り始めてから渡り終わるまでの移動距離は『鉄橋の長さ(550m)＋列車の長さ(Ｌ)』で、この移動距離に30秒かかったということになります。鉄橋の550mを渡るのに30秒ではない点に注意。『渡り終わる』なので、電車の長さＬも加えなければならない。

これを公式にあてはめると、

　速度 ＝ 距離 ÷ 時間
　速度 ＝ (550＋Ｌ) ÷ 30 …(１)

次にトンネルについて考えます。

今度は、トンネルに入り終えてから出始めるまで移動距離というのは、上図を見て頂ければ分かる通り、トンネルの長さ650mから列車の長さＬを引いた距離になります。この距離を移動するのにかかった時間が20秒ということなので公式にあてはめると次のようになります。

　速度 ＝ 距離 ÷ 時間
　速度 ＝ (650－Ｌ) ÷ 20 …(２)

そして、設問にもある通り、速度は一定。要は、鉄橋を渡るときもトンネルを抜けるときも同じ速度という事になる。よって、式(１)の速度と式(２)の速度はイコールになります。よって、次のことが言えます。

　式(１) ＝ 式(２)
　(550＋Ｌ) ÷ 30　＝ (650－Ｌ) ÷ 20

この式を解くと、列車の長さＬが求まります。
式を解くには両辺に60を掛けて割り算を無くすと計算しやすいです。

　(550＋Ｌ) ÷ 30　＝ (650－Ｌ) ÷ 20
　(550＋Ｌ) ÷ 30 × 60　＝ (650－Ｌ) ÷ 20 × 60
　(550＋Ｌ) × 2　＝ (650－Ｌ) × 3
　1100＋2Ｌ ＝ 1950ー3Ｌ
　5Ｌ ＝ 850
　Ｌ ＝ 170

よって、列車の長さは170m

解答：170ｍ

※解説内容に不明な点があればコメント欄にコメントください。