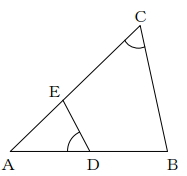
(８) 図のように、ＡＢ＜ＡＣである三角形ＡＢＣにおいて、辺ＡＢ上に点Ｄをとり、辺ＡＣ上に点Ｅを、∠ＡＣＢ＝∠ＡＤＥとなるようにとる。
ＡＢ＝8cm、ＡＤ＝4cm、ＡＥ＝3.2cmのとき、線分ＣＥの長さを求めなさい。
解答と解説
問題の解説：
三角形ＡＢＣの∠ＣＡＢと、三角形ＡＥＤの∠ＤＡＥは、共通なので∠ＣＡＢ＝∠ＤＡＥとなる。更に設問より、∠ＡＣＢ＝∠ＡＤＥだと分かっている。よって、残りの∠ＣＢＡ＝∠ＤＥＡも成り立ちます。
従って、三角形ＡＢＣと三角形ＡＥＤは、相似の三角形。言い換えると、三角形ＡＥＤをＸ倍すると三角形ＡＢＣになる。
辺ＡＤをＸ倍したものが辺ＡＣ ＡＣ＝Ｘ・ＡＤ
辺ＡＥをＸ倍したものが辺ＡＣ ＡＢ＝Ｘ・ＡＥ
辺ＤＥをＸ倍したものが辺ＡＣ ＣＢ＝Ｘ・ＤＥ
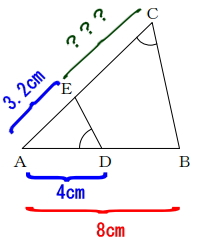
辺ＡＢの長さが8cm、辺ＡＥの長さが3.2cmということより
ＡＢ＝Ｘ・ＡＥ
8＝Ｘ・3.2
Ｘ＝8÷3.2＝2.5
三角形ＡＢＣは、三角形ＡＥＤの2.5倍の大きさということになります。当然、各辺の長さも2.5倍になるため辺ＡＣの長さは、辺ＡＤの2.5倍になる。
ＡＤ・2.5 ＝ ＡＣ
ＡＤは、4cmなので
4・2.5 ＝ ＡＣ
ＡＣ ＝ 10cm
辺ＡＥの長さが3.2cmなので求めたい線分ＥＣの長さは、
ＥＣ＝10ー3.2＝6.8cm
解答：6.8cm
※解説内容に不明な点があればコメント欄にコメントください。
