東京 職業訓練 試験問題[学力検査] 数学-問3(平成29年4月生)

問３ 試験問題

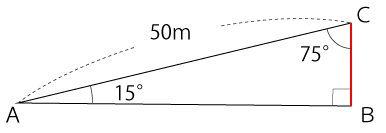
下図のように水平線に対する傾きが15度の斜面を点Ａから点Ｃに50ｍ進んだとき、垂直方向に何ｍ移動しますか。ただし、cos75°＝0.258とします。

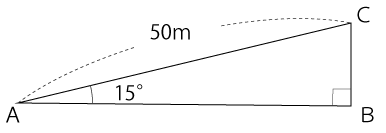
以下は解答と解説です。まずは、解答、解説を見る前に自分自身で解けるかチャレンジしてみてください。

解答と解説

試験問題３の解答：12.9ｍ

問題文にcos75°とあるが、この問題を解くには『cosΘ』が何なのかについて知っておく必要があります。他にもsinθやtanθなどもありますが、この問題に必要なのはcosθに関する知識のみです。

下図のように直角三角形があったとします。

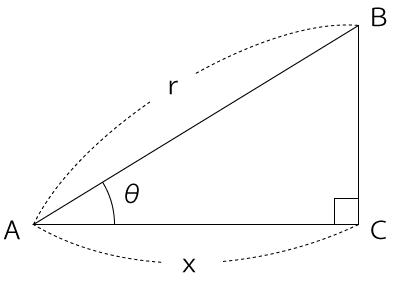
このときのcosθは次のような値になります。

cosθ＝ｘ/ｒ

※直角な∠に対面する辺が分母になる。

このことを知っていれば、この問題は簡単に解くことができます。

知りたいのは点Ａから点Ｃへ進んだときの垂直方向の移動距離です。言い換えると、辺ＢＣの長さのことです。

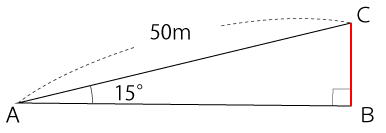
ここで使用するのがcosθなのですが、『cos15°って問題文にないのでわからない！』ってならないでくださいね。

cosθは上記のような式になります。

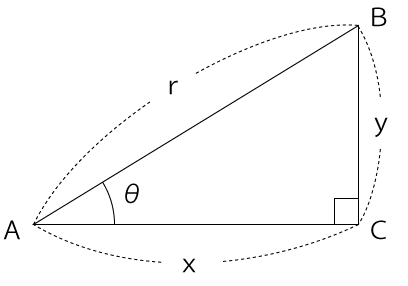
よって、上図のような三角形の場合、cosθは次のようにあらわすことができます。

cosθ＝ｘ/ｒ＝ｙ/ｒ

∠Ｂ＝90°、∠Ａ＝15°と分かっているので∠Ｃ＝75°となります。

これをcosθの式に当てはめると次のようになります。

cos75°＝ＢＣ/50
ＢＣ＝0.258×50
　　＝12.9

よって、もとめる垂直方向の移動距離は12.9ｍ

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。