この問題は平成29年4月入校の東京都立職業能力開発センター入校選考試験問題の問６の解答と解説です。

問１～問６に関しては以下のページに解説をまとめているので参考にして下さい。

実際の試験の問題用紙は以下のページで確認することができます。

⇒都立職業能力開発センター入校選考試験問題(平成29年04月生)

問題を解くのに必要な知識

  • sin60°の値(今回使用)
  • cos60°の値(今回使用)
  • 三平方の定理(今回使用)
  • ヘロンの公式(任意)
  • 余弦定理(任意)

※任意で記載した知識を知っているとより効率的にこの問題を解くことができます。

問６ 試験問題

下図のように１辺の長さが４cmの正四面体ＡＢＣＤがあります。点Ｐは辺ＡＤ上で、ＡＰ：ＰＤ＝１:３の位置にあるとき、三角形ＰＢＣの面積は何cm²ですか。

正四面体

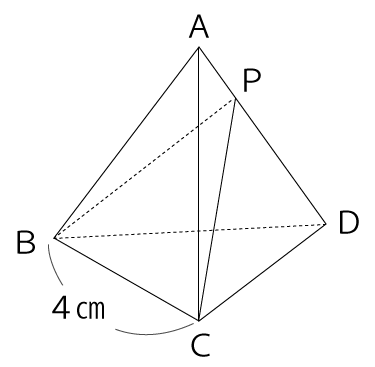
以下は解答と解説です。まずは、解答、解説を見る前に自分自身で解けるかチャレンジしてみてください。

解答と解説

試験問題６の解答：6㎝²

問題文より分かっている部分をすべて図に書き込むと下図のようになります。求めたい三角形PBCの面積がオレンジ色の部分です。

正四面体

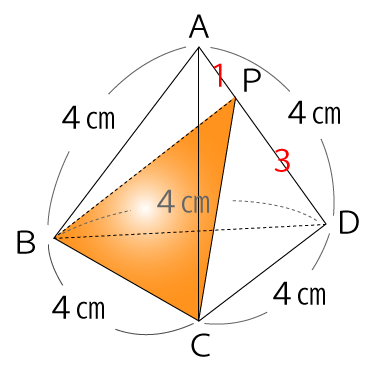
まずは、点Ｐから辺ＣＤに垂線を下ろし交わる点をＱとします。

正四面体

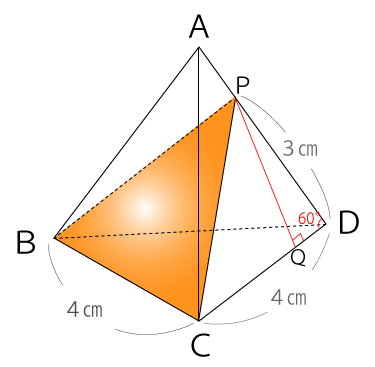
∠D＝60°と分かっているので、下記のように辺ＰＱの長さを求めることができます。

sin60°＝ＰＱ/3
√3/2＝ＰＱ/3
ＰＱ＝3√3/2

同様に変ＤＱの長さも求めます。

cos60°＝ＤＱ/3
1/2＝ＤＱ/3
ＤＱ＝3/2

よって、ＱＣの長さは次のようになります。

ＱＣ＝4-ＤＱ
　　＝4-3/2
　　＝8/2-3/2
　　＝5/2

次に三平方の定理を使用してＰＣの長さを求めます。

ＰＣ²＝ＰＱ²+ＱＣ²
　　＝(3√3/2)²+(5/2)²
　　＝27/4+25/4
　　＝52/4
　　＝13
ＰＣ＝√13

次に点Ｐから辺ＢＣに垂線を下ろし、辺ＢＣと交わる点を点Ｅとします。

正四面体

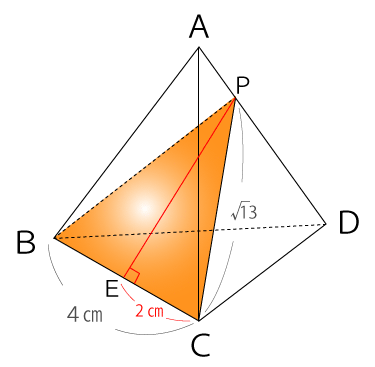
このＰＥの長さを三平方の定理を使用して求めます。

ＰＣ²＝ＰＥ²+ＥＣ²
(√13)²＝ＰＥ²+2²
13＝ＰＥ²+4
ＰＥ²＝9
ＰＥ＝3

このＰＥは三角形ＰＢＣの高さになるので、求めたい三角形ＰＢＣの面積は次のようになります。

△ＰＢＣ面積＝ＢＣ×ＰＥ÷2
　　　　　　＝4×3÷2
　　　　　　＝6

よって、三角形ＰＢＣの面積は6㎝²となります。

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。