この問題は平成31年4月入校の東京都立職業能力開発センター入校選考試験問題の問6の解答と解説です。
問1~問5に関しては以下のページに解説をまとめているので参考にして下さい。
- 東京 職業訓練 試験問題[学力検査] 数学-問1(平成30年04月生)
- 東京 職業訓練 試験問題[学力検査] 数学-問2(平成30年04月生)
- 東京 職業訓練 試験問題[学力検査] 数学-問3(平成30年04月生)
- 東京 職業訓練 試験問題[学力検査] 数学-問4(平成30年04月生)
- 東京 職業訓練 試験問題[学力検査] 数学-問5(平成30年04月生)
実際の試験の問題用紙は以下のページで確認することができます。
問6 試験問題
下の図で、CDは円Oの接線となります。辺BCの長さは何cmですか。
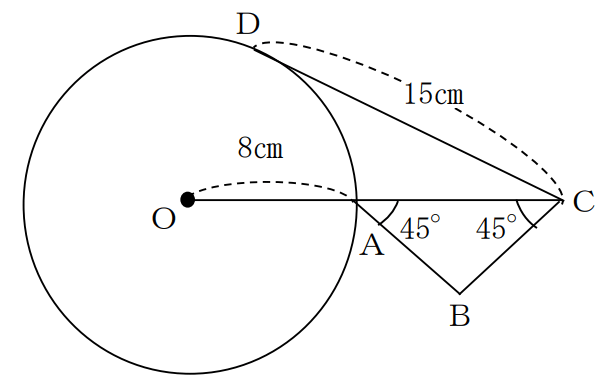
以下は解答と解説ですが、解答・解説を見る前にまずは自分自身でしっかりと考えるようにしてくださいね。
解答と解説
試験問題6の解答:9√22cm
CDは円の接線ということなので、∠CDO=90°となります。これはしっかりと覚えておいてくださいね。円の接線と中心から接点に引いた直線は必ず直角に交わります。
また、ODは円の半径なので8cmだとわかります。
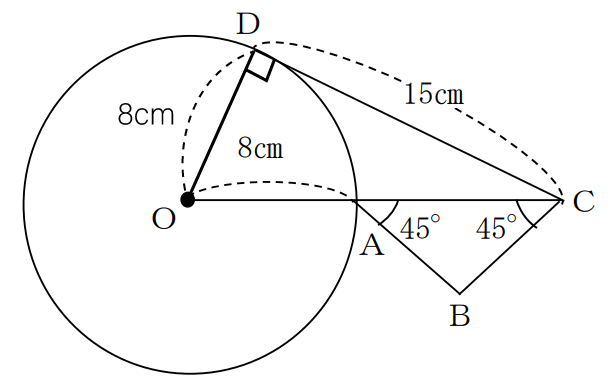
ここで三平方の定理を利用してOCの長さを求めます。
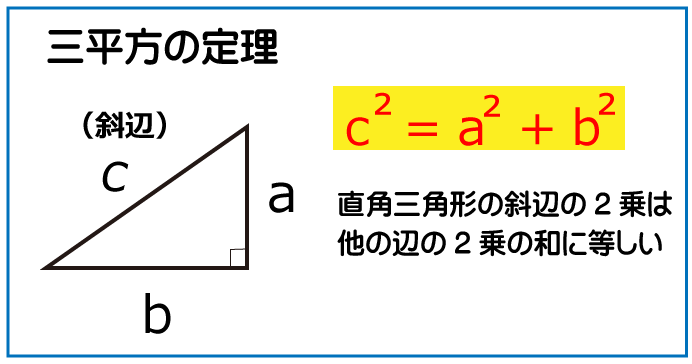
OC²=CD²+OD²
OC²=15²+8²
OC²=225+64
OC²=289
OC=√289
OC=17
よって、CAの長さは次の通り
CA=17-8=9
ここで三角形ABCは直角二等辺三角形なので、各辺の比は次のようになります。
AB:BC:CA=1:1:√2
よって、辺BCの長さは次の式で表すことができます。
BC × √2 = CA
CAの長さは分かっているので、値を代入すると次のようになります。
BC × √2 = 9
BC=9√2
=9√22cm
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。


BC=9/√2まで分かったのですが、その後どのようにして9√2/2となるのか教えて頂けるでしょうか?自力で解決出来ず申し訳ありません。
Y.S様
ご質問ありがとうございます。
9/√2のように解答の分母にルートが残ったままだと不正解扱いにされるため(問題用紙の注意事項欄に分母にルートが残したらだめと記載されています)、ルートを外す必要があります。√2のルートを外すには√2を掛ければ√2×√2=2となり、ルートがはずれます。
しかし、分母だけに√2を掛けると値そのものが変わってしまい、解答結果が異なる値になってしまいます。
9/(√2×√2) =9/2 ≠ 9/√2
そこで、分母と分子の両方に√2を掛けます。要は、√2/√2を掛けるという事です。√2/√2は約分すると1です。1はどんな数値に掛けても元の数値を変化させることはないので、解答値を違う値に変えてしまうことはありません。
(9/√2) × 1 = 9/√2
ですよね。 よって、次のことも同じことを意味します。
(9/√2) × (√2/√2) = 9√2/2
「9/√2」の値と、「9√2/2」の値は見た目こそ違いますが、同じ数値になります。
ODは円の半径なので8cmというのがよく分かりません。
RG様
ご質問ありがとうございます。
ODが何故、円の半径になるかが分からないということでしょうか?それとも何故、8cmになるかが分からないということでしょうか?
途中の計算のBCの長さを出すところBC × √2 = CAとなるのはなぜでしょうか
ご質問ありがとうございます。
AB:BC:CA=1:1:√2
まず、わかりやすく説明するために上記の各辺の比のAB:BCだけに着目してみてください。そうすると、以下の式になります。
AB:BC=1:1
これは、ABとBCの比率が1:1で同じ長さと言うことがわかりますよね。よって、それを式に表すと次のようになります。
AB=BC
解説の中で記載している「BC × √2 = CA」もこの考え方からきています。先程と同様に今度は、BCとCAの比率に着目すると以下のようになります。
AB:BC:CA=1:1:√2
↓
BC:CA=1:√2
これは、BCの長さが1に対して、CAの長さは√2 あると言うことを意味しています。要は、CAの長さはBCの長さの√2倍と言うことです。よって、BCの長さを√2倍すればCAの長さと等しくなるので、以下の式が成り立ちます。
BC × √2 = CA
できれば上記の本質を理解はしていおいた方が良いとは思いますが、本番で上記を考えて解いていると時間のロスになるので、以下の考えを覚えておけば一瞬で式を導き出せます。
「(式の内側を掛ける)=(式の外側を掛ける)」
式の内側と言うのは、
BC:CA=1:√2
このばあいであれば、「CA」と「1」になります。そして、外側と言うのは「BC」と「√2」になります。よって、次のようになります。
「(式の内側を掛ける)=(式の外側を掛ける)」
(CA×1)=(BC×√2)
CA=BC×√2
289が17になる理由が分かりません。
平方根を求めようとしても最初に3で割ってしまうので17が考えつきづらいと思うのですがなにか他に√を求める方法があるのでしょうか?
ご質問ありがとうございます。
289は3では割れませんよね。
本来であれば、2.3.5.7.11.13.17.19.23.・・といった素数と言われる数値を2乗した結果を頭に入れておくのがベストです。一般的には17の2乗あたりまでは覚えておいた方がいいと言われています。ただ、覚えていなくても求めることは可能です。例えば、今回の289であれば1桁目が「9」です。なので、同じ数字を掛け算して1桁目が9になる数値と言えば、1桁目に3もしくは7が付く数値しかありません。3、7、13、17、23、27、33・・・ですね。
よって、
3x3=9
7x7=49
13x13=169
17x17=289
と順番に探っていくことで求められます。