東京 職業訓練 試験問題[筆記試験] 数学-問2(3)～(5)【平成30年1月生】

試験問題 問２(３)

一辺が10㎝の正方形ＡＢＣＤがあります。図のように頂点Ａ、Ｃを中心とする半径10㎝、中心角90度のおうぎ形をかきます。斜線部の面積は何㎝²ですか。

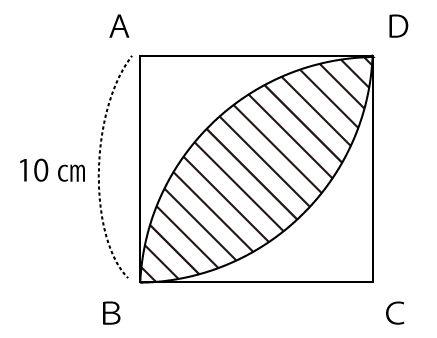
解答と解説

問２(３)の解答：50π－100 ㎝²

まずは、点Ｃを中心とした半径10㎝、中心角90度の扇形の面積を求めます。

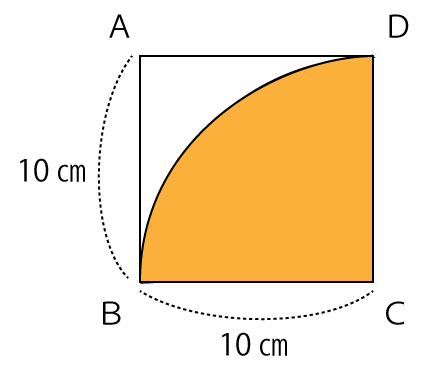
扇形の面積は半径10㎝の円の面積の1/4になります。
扇形BCDの面積＝(半径×半径×π)÷4
　　　　　　　＝100π÷4
　　　　　　　＝25π

この扇形の面積から△BCDの面積を引けば、下図の部分の面積が求まります。

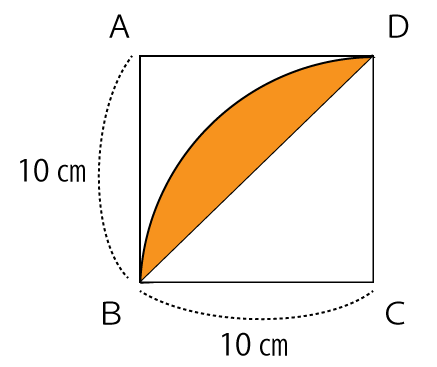
△BCDの面積＝底辺×高さ÷2
　　　　　＝10×10÷2
　　　　　＝50

よって、上図のオレンジ色部分の面積は次の通り。
面積＝25π－50

問題の斜線部の面積はこのオレンジ色部分の2倍に相当するので、求める斜線部の面積は次の通り。

斜線部の面積＝(25π－50)×2
　　　　　　＝50π－100 ㎝²

試験問題 問２(４)

赤い玉が２個、白い玉が２個、青い玉が２個入った袋があります。この袋の中から玉を３個同時に取り出したとき、３個とも異なる色の玉である確率を分数で求めなさい。

解答と解説

問２(４)の解答：2/5

この問題を解くには、組み合わせ数を求める公式を知っている必要があります。

全玉数6個から3個を取り出す組み合わせ数は、以下の通りです。

全玉数6個から3個を取り出す組み合わせ数＝₆Ｃ₃
₆Ｃ₃＝(6×5×4×3×2×1)/{(3×2×1)×(3×2×1)}
　　＝(6×5×4)/(3×2×1)
　　＝120/6
　　＝20通り

3色とも異なる色ということは、各色2個から1個ずつ選ばれることになります。よって、その組み合わせ数は次の通り。

₂Ｃ₁×₂Ｃ₁×₂Ｃ₁＝{(2×1)/(1×1)}×{(2×1)/(1×1)}×{(2×1)/(1×1)}
　　　　　　　＝2×2×2
　　　　　　　＝8通り

よって、全20通りの中から各色1個ずつ取り出す確率は8/20＝2/5

試験問題 問２(５)

図のように平行な２直線l、mがあるとき、∠Ｘは何度ですか。

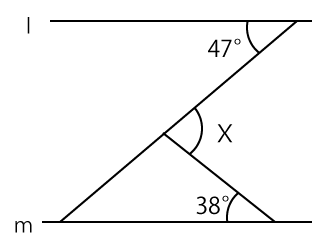
解答と解説

問２(５)の解答：85°

この問題は、下図のＭの角度を求めたら以下の式でＸの角度が求まります。

Ｘ＝Ｍ＋38

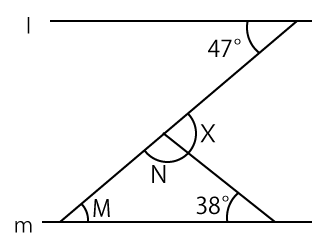
Ｎを求めてから180－ＮでＸの角度を求めていると若干のタイムロスが発生するので、『Ｘ＝Ｍ＋38』が成り立つことをしっかりと頭にいれておいてください。

ｌとｍは平行線なのでＭ＝47°となります。よって、Ｘの角度は次の通り。

Ｘ＝Ｍ＋38
　＝47＋38
　＝85°

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。