この問題は令和元年7月入校の東京都立職業能力開発センター入校選考試験問題の問2の(1)と(2)の解答と解説です。
問1および問2の(3)~(5)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
■目次
試験問題 問2(1)
自宅から目的地の駅までの道のりは114kmあります。自宅から最寄り駅まで時速5kmで歩き、残りを時速70kmの電車で移動しました。移動時間の合計は2時間でした。自宅から最寄り駅までの道のりは何kmであるか求めなさい。
※以下は解答と解説ですが、見る前にまずは、自分自身でしっかりと解いてみてください。
解答と解説
問2(1)の解答:2Km
この問題を解くには、速度と距離と時間の関係式を知っておく必要があります。

こういった問題は問題用紙の余白に図式化することが大切です。求めたい自宅と最寄り駅までの距離をX㎞とし、その他問題から分かっている点を図に書き込むと下図のようになります。
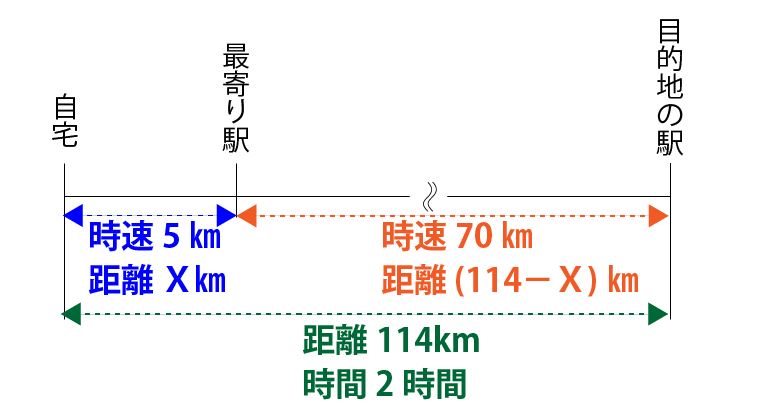
自宅~最寄り駅までの時間を求める
まずは、自宅から最寄り駅までの時間を求めます。公式より以下の式が成り立ちます。
時間=距離 ÷ 速度
=X ÷ 5
=X5
最寄り駅~目的地の駅までの時間を求める
最寄り駅から目的地の駅までにかかる時間を求めます。公式より以下の式が成り立ちます。
時間=距離 ÷ 速度
=(114-X) ÷ 70
=(114-X)70
自宅~最寄り駅までの距離を求める
自宅から最寄り駅までの時間は、5X。最寄り駅から目的地の駅までにかかる時間は、7980-70Xと分かりました。自宅から目的地の駅までにかかる時間は設問より2時間と分かっています。よって、以下の式が成り立ちます。
X5 + (114-X)70= 2
この式を解くと求めたい回答Xがでてきます。
X5 + (114-X)70= 2
両辺に70を掛けて分数を無くします。
14X + (114-X) = 140
13X = 26
X = 2
よって、自宅から最寄り駅までの距離は2Km
試験問題 問2(2)
あるクラス20人全員でソフトボール投げをしました。クラス全員の記録の平均は35mであり、またそのうちの2人を除いた記録の平均は34mでした。この除いた2人の記録の平均は何mか求めなさい。
※以下は解答と解説ですが、見る前にまずは、自分自身でしっかりと解いてみてください。
解答と解説
問2(2)の解答:44m
20人の平均は35mです。よって、平均ではなく20人の合計記録は次の式で表すことができます。
平均値=合計記録÷人数
合計記録=人数×平均値
よって、
合計記録=20人×35m=700m
次に2人を除いた18人の平均は34mなので、同様に合計記録は次のようになります。
合計記録=18人×34m=612m
ここで除いた2人の合計記録をXとすると、以下の式が成り立ちます。
612m+ X = 700m
X=88m
求めたいのは除いた2人の平均記録なので、合計記録を2で割れば平均がでます。
除いた2人の平均記録=88 ÷ 2
=44m
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

