この問題は令和元年7月入校の東京都立職業能力開発センター入校選考試験問題の問2の(3)と(4)の解答と解説です。
問1および、問2の(1)(2)(5)(6)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
■目次
試験問題 問2(3)
図のような1辺8cmの正方形内部に,点A,Cを中心とする半径8cmの円の弧がかかれています。斜線をつけた部分の面積は何cm²であるか求めなさい。
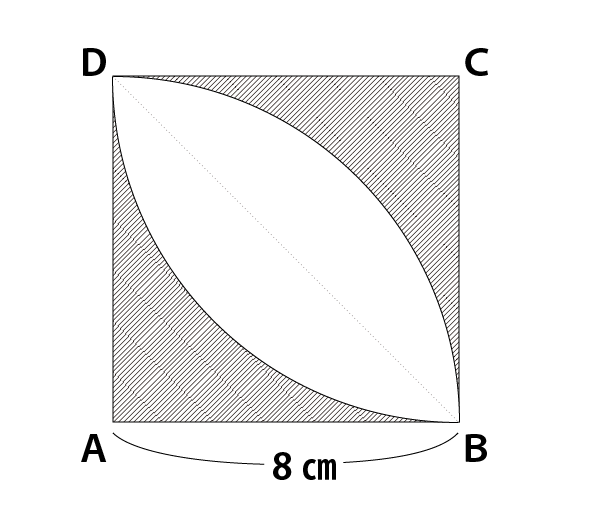
※以下は解答と解説ですが、見る前にまずは、自分自身でしっかりと解いてみてください。
解答と解説
問2(3)の解答:(128-32π) cm²
考え方としては、正方形ABCDの面積から白塗りの部分の面積を引いて斜線部分の面積を求めます。
正方形ABCDの面積を求める
一辺が8cmの正方形なので、面積は次の通り。
ABCDの面積=8×8=64cm²
扇形ABDの面積を求める
扇形ABDの面積は点Aを中心とする半径8cmの円の面積の1/4の大きさになります。
点Aを中心とする半径8cmの円の面積
=半径×半径×π
=8×8×π
=64π cm²
扇形ABDの面積はこの円の1/4の大きさなので次の通りになります。
扇形ABDの面積=64π÷4=16π cm²
三角形ABDの面積を求める
三角形ABDの面積は次の通り。
三角形ABDの面積
=底辺×高さ÷2
=8×8÷2
=32 cm²
白塗りの面積を求める
先程求めた扇形ABDの面積から三角形ABDの面積を引くと下図の白色部分の面積が求まります。
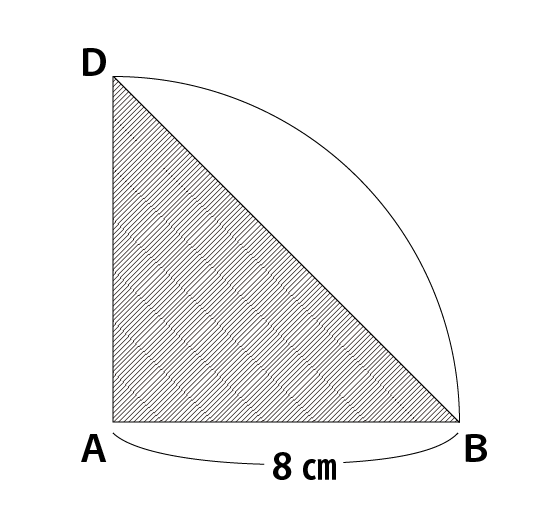
白色部分の面積=(16π-32) cm²
しかし、求めたい白塗りの部分は下図の場所なので実際は上記面積の2倍の大きさになります。
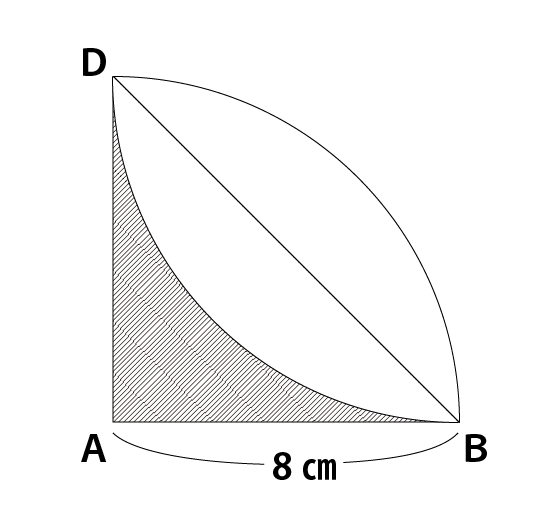
よって、求めたい白塗りの面積は次の通り。
(16π-32)×2 cm²
=(32π-64) cm²
斜線部分の面積を求める
斜線部分の面積は正方形ABCDの面積から白塗りの面積を引いた大きさなので、次の式が成り立ちます。
斜線部分の面積=64-(32π-64)
=(128-32π) cm²
試験問題 問2(4)
みかん味のキャンディが3つ,リンゴ味のキャンディが2つあります。この5つのキャンディの中から同時に2つ取るとき,少なくとも1つがみかん味のキャンディとなる確率を分数で求めなさい。
※以下は解答と解説ですが、見る前にまずは、自分自身でしっかりと解いてみてください。
解答と解説
問2(4)の解答:910
まずは、5つのキャンディの中から2つの取る場合の総組み合わせ数を求めます。そして、その総組み合わせ数の中からみかん味のキャンディが含まれる組み合わせ数を求めれば、以下の式でみかん味のキャンディが含まれる確率を求めることができます。
みかん味のキャンディが少なくとも1つ含まれる確率
=(みかん味のキャンディが含まれる組み合わせ数)÷(総組み合わせ数)
総組み合わせ数を求める
5つのキャンディの中から2つを抜き出す組み合わせ数は、組み合わせ数の公式で求めることができます。

₅C₂=5!2!(5-2)!
=5×4×3×2×1(2×1)(3×2×1)
=10通り
みかん味のキャンディが含まれる組み合わせ数を求める
『みかん味のキャンディが含まれる組み合わせ数』というのは、要は『取ったキャンディがすべてりんご味』にならない限り、これに該当します。
取った2つのキャンディが両方ともリンゴ味になる組み合わせ数は次の通り。
₂C₂=2!2!(2-2)!
=2×1(2×1)(1)
=1通り
補足
『0!』は0ではなく1になる。
取ったキャンディが全てりんご味になるのは1通りのみ。よって、全10通りの内、9通りは少なくとも1個はみかん味が含まれることになります。
みかん味が含まれる確率を求める
全10通りの内、9通りは少なくとも1個はみかん味が含まれるので、その確率は次の通り。
みかん味が1個以上含まれる確率
=910
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

