東京 職業訓練 試験問題[筆記試験] 数学-問2(5)【令和元年7月生】

試験問題 問２(５)

２枚１組の三角定規を右の図のように並べ，四角形ＡＢＣＤを作りました。ＡＣ＝18cmのとき，四角形ＡＢＣＤ面積は何cm²であるか求めなさい。

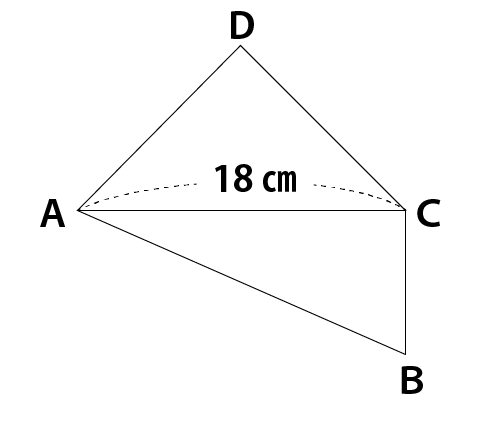
※以下は解答と解説ですが、見る前にまずは、自分自身でしっかりと解いてみてください。

解答と解説

問２(５)の解答：81＋54√3 cm²

個人的には少し不親切な問題だと思っているのですが、設問で言われている2枚の三角定規は、角が45°・45°・90°の直角二等辺三角形と、角が30°・60°・90°の直角三角の定規2枚を意味しています。よって、この点を知らないとこの問題を解くことはできません。

この問題は以下の特別な三角形の比を知っていることで解くことができます。

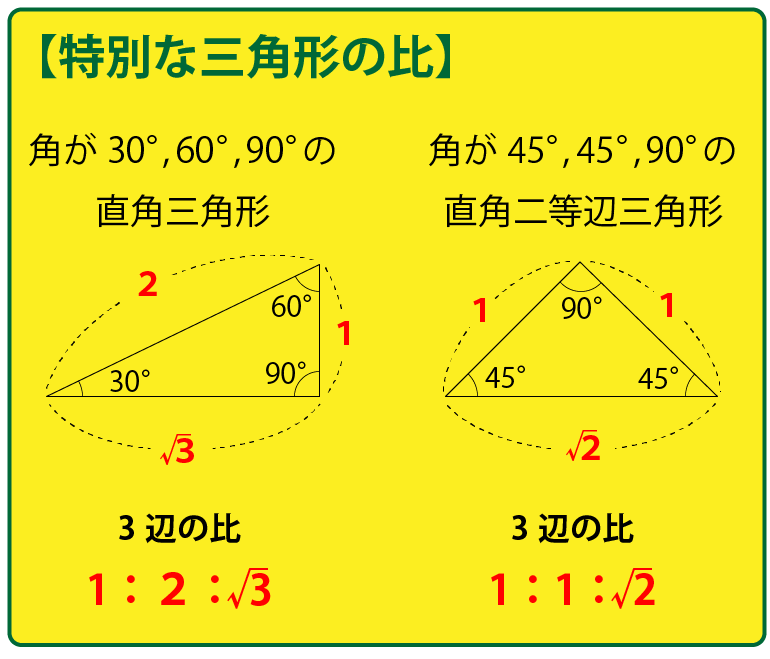
直角二等辺三角形ACDの面積を求める

AD：CD：AC＝1：1：√2 なので、ADとCDの長さは次の通り。

AD：AC＝1：√2
AD：18＝1：√2
√2AD＝18
AD＝18√2

AD=CD＝18√2

よって、三角形ACDの面積は次の通り。

三角形ACDの面積＝18√2 × 18√2 ÷ 2
　　　　　　　　＝18×182 ÷ 2
　　　　　　　　＝81

直角三角形ABCの面積を求める

BC：AB：AC＝1：2：√3
BC：AC＝1：√3
BC：18＝1：√3
√3BC＝18
BC＝18√3

よって、直角三角形ABCの面積は次の通り。

直角三角形ABCの面積＝18√3 × 18 ÷ 2
　　　　　　　　　　＝18√33 × 18 ÷ 2
　　　　　　　　　　＝18√3 × 6 ÷ 2
　　　　　　　　　　＝54√3

四角形ABCDの面積を求める

四角形ABCDの面積＝△ACD＋△ABC
　　　　　　　　＝81＋54√3 cm²

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。