東京 職業訓練 試験問題[筆記試験] 数学-問2(1)(2)【令和元年10月生】

試験問題 問２(１)

図は、四角形ＡＢＣＤに対角線ＢＤをひいた図です。ＡＢ＝ＡＤ、∠ＤＡＢ＝∠ＣＤＢ＝90°、∠ＤＢＣ＝30°、ＤＣ＝２cmであるとき，四角形ＡＢＣＤの面積は何cm²
であるか求めなさい。

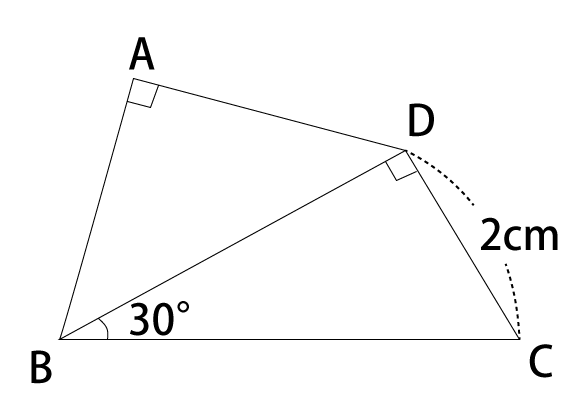
※以下は解答と解説ですが、見る前にまずは、自分自身でしっかりと解いてみてください。

解答と解説

問２(１)の解答：3+2√3 cm²

この問題を解くには、以下の三平方の定理、もしくは、特別な三角形の比を知っていることで解くことができます。

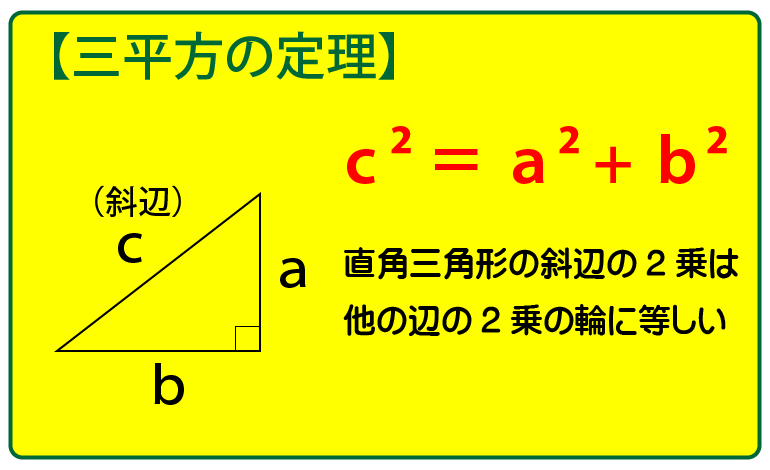
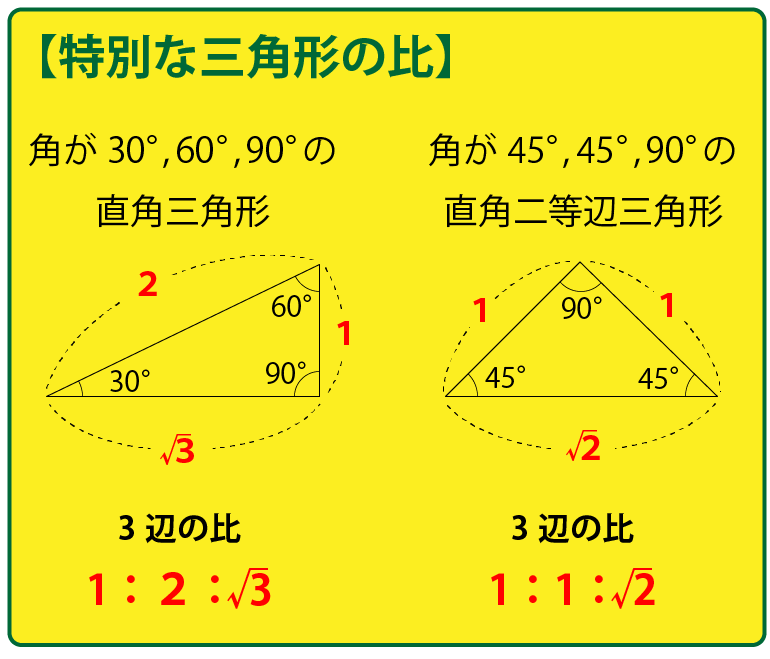
△BCDの面積を求める

∠DBC＝30°、∠CDB＝90°なので、∠BCD＝60°だと分かります。よって、『特別な三角形の比』が適用できるので、各辺の長さの比は次のようになります。

CD：BC：BD＝1：2：√3

CDの長さは2cmなので、BCとBDの長さは次の通り。

BCの長さはCDの2倍なので、4cm。
BC＝4cm

BDの長さはCDの√3倍なので、2√3。
BD＝2√3

△BCDは、底辺がCDで高さがBDの直角三角形です。よって、その面積は次の通り。

△BCDの面積＝底辺×高さ÷2
　　　　　　＝2×2√3÷2
　　　　　　＝2√3 cm²

△ABDの面積を求める

問題文よりAB＝AD、∠A＝90°と分かっているので△ABDは直角二等辺三角形になります。よって、△ABDも『特別な三角形の比』が適用できます。各辺の比は次の通り。

AB：AD：BD＝1：1：√2

BDの長さは先程、2√3と分かりました。よって、ABとADの長さは次の通り。

BDの長さはABの長さの√2倍。言い換えると、ABの長さは、BDの長さの1√2倍です。

よって、ABの長さは以下の通り。

AB＝BDの長さ×1√2
　＝2√3×1√2
AB＝2√3√2

ADの長さはABの長さと等しいので、ADの長さも以下となります。
AD＝2√3√2

△ABDは底辺AB、高さADの直角二等辺三角形です。よって、その面積は次の通り。

△ABDの面積＝底辺×高さ÷2
　　　　　　＝AB×AD÷2
　　　　　　＝2√3√2×2√3√2÷2
　　　　　　＝122÷2
　　　　　　＝6÷2
　　　　　　＝3 cm²

四角形ABCDの面積

四角形ABCDの面積は、△ABDと△BCDの面積の合計に等しいので次の通り。

四角形ABCDの面積＝△ABD+△BCD
　　　　　　　　＝3+2√3 cm²

試験問題 問２(２)

文房具店でクレヨン12本と120円のボールペン1本を買いました。この代金の合計は、クレヨン2本と60円の消しゴム1個の代金の合計の4倍と同じでした。クレヨン1本の代金は何円であるか求めなさい。ただし，消費税は考えないものとします。

※以下は解答と解説ですが、見る前にまずは、自分自身でしっかりと解いてみてください。

解答と解説

問２(２)の解答：30円

求めたいクレヨン1本の代金をＮ円と仮定します。
クレヨン12本と120円のボールペン1本の合計代金は、クレヨン2本と60円の消しゴム1個の代金の合計の4倍と等しいということなので以下の式が成り立ちます。

(12×Ｎ)+(1×120)＝｛(2×Ｎ)+(1×60)｝×4

この式を解くと求めたいクレヨン1本の値段Ｎ円が求まります。

(12×Ｎ)+(1×120)＝｛(2×Ｎ)+(1×60)｝×4
12Ｎ+120＝(2Ｎ+60)×4
12Ｎ+120＝8Ｎ+240
4Ｎ＝120
Ｎ＝30

よって、クレヨン1本の値段は30円

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。