次の図のように、1段目に1個、2段目に3個、3段目には5個、・・・という規則に従って、奇数個のご石を順に置いていく。このとき、次の各問の答えとして正しいものをア~オの中から 1 つ選び、記号で答えなさい。
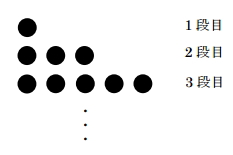
[問題1]14 段目までご石を並べたとき、全部で何個のご石を使うか求めなさい。
ア 180個
イ 186個
ウ 190個
エ 196個
オ 200個
[問題2]n段目から25段目のご石の合計が225個である。このとき、nに当てはまる数を求めなさい。
ア 13
イ 15
ウ 17
エ 19
オ 21
解答と解説
問題1の解説:
格段のご石の数は、次のように増えていきます。
1段目 1
2段目 3
3段目 5
4段目 7
5段目 9
6段目 11
7段目 13
……
上記は、格段のご石の数ですが、各段までのご石の合計は次のように増えていきます。
1段目の合計数 1
2段目までの合計数 4
3段目までの合計数 9
4段目までの合計数 16
5段目までの合計数 25
6段目までの合計数 36
7段目までの合計数 49
……
ここである法則に気が付けばこの問題は解けたも同然です。各段までの合計数は、その段の2乗に等しい数値になります。
よって、14段目までのご石の合計は、
14段目までのご石の合計=14²=196
よって、求める解答は196個のエ
解答:エ
問題2の解説:
問題1の考え方で解くことができます。
25段目までのご石の合計は、
25段目までのご石の合計=25²=625
625と分かりました。これは、1段目から25段目までの合計です。しかし、設問はn段目から25段目でご石の合計が225個となるようなnを求めたい。
625-225=400
となるので、1段目からのご石の合計が400となるような段数を求めます。段数の2乗が合計ご石数なので1段目から20段目までの合計が400だとすぐに分かります。
よって、1段目から20段目を取り除いた21段目から25段目までのご石合計が225となります。
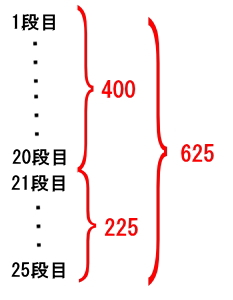
求めたい解答は、21段目のオ
解答:オ
※解説内容に不明な点があればコメント欄にコメントください。

