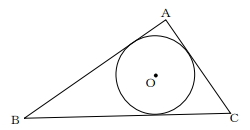
(4)下図の円Oは、∠A=90°の三角形ABCの内接円である。AB=12cm、AC=9cmのとき、円Oの半径を求めなさい。
解答と解説
試験問題の解答:3 cm
三角形に内接する円の半径は、三角形の面積と関連付けて求めることができます。
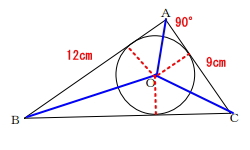
上図のように三角形OAB、OBC、OCAの3つに分けて考えます。
まずは、三角形OBCに着目。
点Oから辺BCに垂直に下ろした線が三角形OBCの高さであり、円の半径になります。そして、この三角形OBCの面積は次の式で表すことができます。
三角形OBCの面積=辺BC×円の半径÷2
底辺となる辺BCの長さが分からないので求めます。三角形ABCは、∠Aが90°となる直角三角形なので三平方の定理を使用して辺BCの長さを求めることができます。
三平方の定理
C²=A²+B²
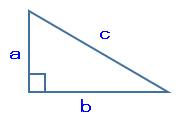
よって、三角形ABCを三平方の定理にあてはめると次のようになります。
BC²=AB²+AC²
BC²=12²+9²=144+81=225
BC=√225=15
同様に残り2つの三角形の面積は次の式で表すことができます。
三角形OABの面積=辺AB×円の半径÷2
三角形OCAの面積=辺CA×円の半径÷2
そして、三角形ABCの面積はこれら3つの三角形の合計になるので次の式で表すことができます。
三角形ABCの面積=三角形OBCの面積+三角形OABの面積+三角形OCAの面積
=(辺BC×円の半径÷2)+(辺AB×円の半径÷2)+(辺CA×円の半径÷2) ・・・(1)
ここで、三角形ABCは、底辺を辺ABとすると高さが辺ACとなります。辺ABの長さは12cm、辺ACの長さは9cm。よって、三角形ABCの面積は次の通り。
三角形ABCの面積=12×9÷2=54cm²
よって、式(1)は次のようになります。
三角形ABCの面積=(辺BC×円の半径÷2)+(辺AB×円の半径÷2)+(辺CA×円の半径÷2) ・・・(1)
54=(辺BC×円の半径÷2)+(辺AB×円の半径÷2)+(辺CA×円の半径÷2)
54=(15×円の半径 ÷2)+(12×円の半径÷2)+(9×円の半径÷2)
式が見難いので×円の半径=rと置き換えます。(別に置きかえなくてもOKです)
54=7.5r+6r+4.5r
54=18r
r=3

