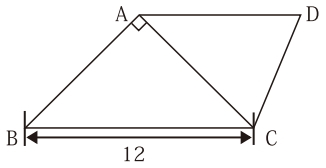
(4)下の図においてAD//BC、AB=AC=AD、∠BAC=90° である。BC=12cmのとき、三角形ACDの面積を求めなさい。
解答と解説
試験問題の解答:18√2
この問題は、正弦定理、余弦定理を使用して求める方法、三角形ACDの3つの辺の長さを求めてヘロンの公式を使う方法などいくつかの解き方があります。しかし、ここでは公式を使用せずに求める方法で解きます。
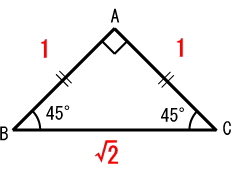
とは言っても、1つだけ知っておく定義があります。それは、直角二等辺三角形の各辺の長さの比は、『1:1:√2』ということです。
それでは、問題の解説に入ります。
三角形ABCは、∠BAC=90°、AB=ACということより、直角二等辺三角形だとわかります。よって、『1:1:√2』の定義が使えます。よって、辺AB、AC、の長さを√2倍した長さが辺BCの長さとなります。辺AB、ACの長さをNとした場合、辺BCが12cmなので、次の式が成り立ちます。
N×√2=12
N=12÷√2
よって、辺AB、AC、ADの長さは、12/√2 となります。また、三角形ABCは直角二等辺三角形なので、∠ABC=∠ACB=45° となります。また、辺BC//辺AD なので∠CADも45°だと分かります。
求めたいのは三角形ACDの面積なので、三角形の底辺をACとした場合、D点から辺ACに向かって垂直に下ろした線が高さとなります。D点から辺ACに向かって垂直に下ろした線が辺ACと交わる点を辺Eとした場合、分かっている内容を整理すると下図のようになります。
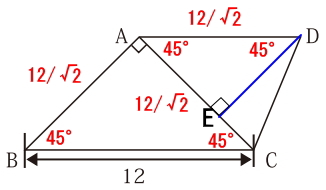
三角形AEDも直角二等辺三角形なので、『1:1:√2』の定義が使えます。
辺AE、DEの長さをMとした場合、辺ADの長さが12/√2なので次の式が成り立ちます。
M×√2=12/√2
M=12/(√2×√2)
M=12/2=6
よって、三角形ACDの底辺ACの長さが12√2、高さDEが6と分かったので、三角形ACDの面積は次の通りになります。
12/√2 × 6 ÷ 2 = 36/√2
解答としてはこのままでもいいのですが、上記の答えは下記のようにも変形できます。
36/√2=18×√2×√2 / √2 =18√2
通常はこのように分数ではなく整数の形になおして解答します。

