この問題は平成30年4月入校の東京都立職業能力開発センター入校選考試験問題の問２の解答と解説です。

問１、問３～問６に関しては以下のページに解説をまとめているので参考にして下さい。

実際の試験の問題用紙は以下のページで確認することができます。

⇒都立職業能力開発センター入校選考試験問題(平成30年04月生)

問題を解くのに必要な知識

  • 扇形の面積を求める公式
  • 円の面積を求める公式

※どちらか一方を知っていれば解くことが可能です。

問２ 試験問題

半径20㎝、中心角108度のおうぎ形の面積は何㎝²ですか。

解答と解説

試験問題２の解答：120π

こういった問題は、まずは図を問題用紙の余白に書く癖をつけましょう。問題文から分かっている点を実際に図形にしたものが下図です。

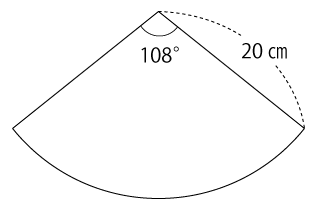
扇形の面積

扇形の面積を求める公式を知っていれば簡単に解ける問題です。扇形の面積の公式は次の通り。

扇形の面積の公式

この公式を使って扇形の面積を求めていきます。

Ｓ＝πｒ²×α/360
　＝π×(20)²×108/360
　＝400π×108/360
　＝400π×3/10
　＝40π×3
　＝120π ㎝²

公式を忘れてしまった場合の解き方

頻繁に使う公式でない場合はなかなか覚えられませんよね。しかし、公式はあくまで計算の過程を簡潔に整理してまとめているものであり、本来の解き方を知っていれば公式は自ら導くことができます。

では、扇形の面積を求める公式を覚えていない、忘れてしまった場合の解き方を解説していきます。

まずは、下図のような半径20㎝の円の面積を求めます。

円の面積

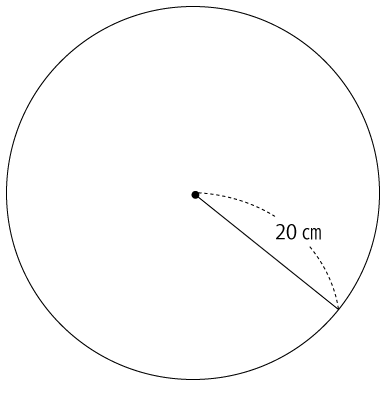
円の面積＝半径×半径×π
　　　　＝20×20×π
　　　　＝400π

扇形はこの真円の一部です。

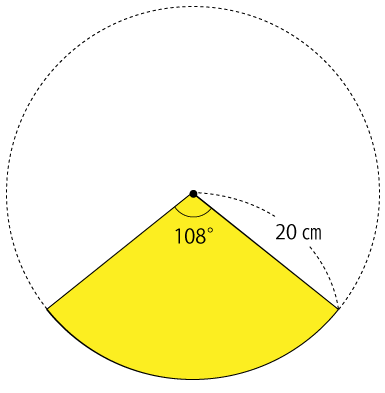
真円と扇形

では、この扇形は真円に対してどのくらいの大きさかというと、中心角が360°の真円に対して、扇形は108°なので扇型の大きさは下記の通りになります。

扇型の大きさ＝108/360
　　　　　　＝3/10

よって、扇形は半径20cmの真円を3/10にした大きさだと分かります。円の面積が400πなので、扇形の面積は次の通り。

扇形の面積＝400π×3/10
　　　　　＝120π ㎝³

公式を用いた解き方と比較して見て頂ければわかると思いますが、やっていることは全く同じです。

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。