この問題は平成30年4月入校の東京都立職業能力開発センター入校選考試験問題の問３の解答と解説です。

問１、問２、問４～問６に関しては以下のページに解説をまとめているので参考にして下さい。

実際の試験の問題用紙は以下のページで確認することができます。

⇒都立職業能力開発センター入校選考試験問題(平成30年04月生)

問題を解くのに必要な知識

知っておかないとダメな公式などは特にありません。

問３ 試験問題

赤玉と白玉と青玉の３種類を袋に入れ、この袋の中から玉を１個取り出すとき、赤玉が出る確率を1/5となるようにします。白玉を70個、青玉を50個入れたとき、赤玉は何個入れればいいですか。

解答と解説

試験問題３の解答：30個

この問題は一見難しく考えてしまいますが、実はいたって簡単な問題です。

赤玉と白玉を取り出す確率といったように組み合わせを考えなければならない問題の場合は組み合わせの公式なども必要になってきますが、この問題は組み合わせなどを考える必要はなく公式も特に使用しません。

まずは、以下の例を考えてみてください。
袋の中に赤玉、青玉、白玉の3個が入っており、その中から1個取り出したとき、赤玉が出る確率はいくつでしょうか？

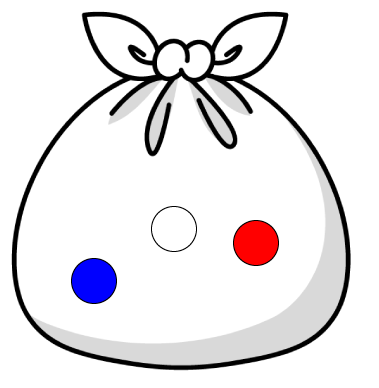
袋から玉を取り出す確率

簡単ですよね？
赤玉が出る確率は1/3です。

このように袋の中から赤玉を取り出す確率は次の式で求まります。

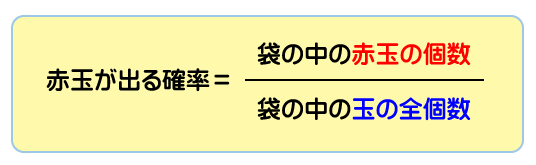
確率の公式

よって、袋の中の赤玉の個数を求めるには、『赤玉が出る確率』と『袋の中の玉の全個数』が分かる必要があります。そして、これらは問題文から既に分かっています。

求めたい袋の中の赤玉の個数をＸと仮定します。

赤玉が出る確率＝1/5
袋の中の玉の全個数＝70+50+Ｘ

よって、袋の中の赤玉の個数は次の式で求まります。

赤玉が出る確率＝(袋の中の赤玉の個数)/(袋の中の玉の全個数)
1/5＝Ｘ/(70+50+Ｘ)
1/5＝Ｘ/(120+Ｘ)
(120+Ｘ)＝5Ｘ
4Ｘ＝120
Ｘ＝30

よって、袋の中の赤玉の個数は30個

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。