この問題は平成30年4月入校の東京都立職業能力開発センター入校選考試験問題の問５の解答と解説です。

問１～問４、問６に関しては以下のページに解説をまとめているので参考にして下さい。

実際の試験の問題用紙は以下のページで確認することができます。

⇒都立職業能力開発センター入校選考試験問題(平成30年04月生)

問題を解くのに必要な知識

  • 三角形の相似条件

問５ 試験問題

長方形ＡＢＣＤの辺ＡＢ上に線分ＡＥ＝40cmになるような点Ｅを取り、下図のように折り返しました。このとき、点Ａが辺ＢＣ上にくる点をＡ’とします。線分ＢＡ’の長さは何cmですか。

長方形

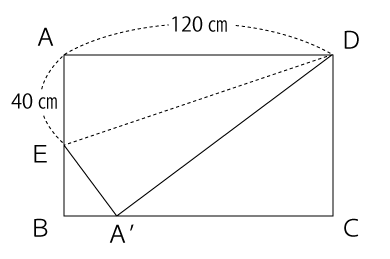
以下は解答と解説ですが、解答・解説を見る前にまずは自分自身でしっかりと考えるようにしてくださいね。

解答と解説

試験問題５の解答：24㎝

既に分かっている点を図に書き込みます。

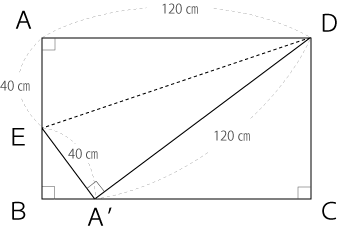
四角形を折りたたんだ図形

ここで気が付いて欲しいのが、『△A’EBと△DA’Cは相似な三角形なのでは？』という点です。

２つの三角形が相似になる条件は次の通り。

三角形の相似条件

  • 3組の辺の比がすべて等しい
  • 2組の辺の比が等しく、その間の角が等しい
  • 2組の角がそれぞれ等しい

それでは、実際に相似な三角形か確認していきます。

∠DA’C＝180°-90°-∠CDA’
　　　＝90°-∠CDA’・・・①

さらに∠DA’Cは、次のようにあらわすこともできます。

∠DA’C＝180°-90°-∠BA’E
　　　＝90°-∠BA’E・・・②

よって、①②から次の式が成り立ちます。

①＝②
90°-∠CDA’＝90°-∠BA’E
∠CDA’＝∠BA’E

よって、『2組の角がそれぞれ等しい』という三角形の相似条件を満たしているのでこの2つの三角形は相似な三角形になります。

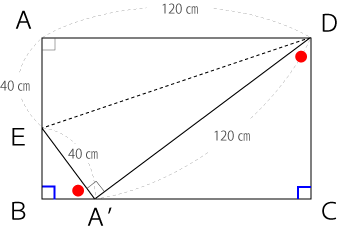
相似な三角形の証明

相似な三角形は、各辺の比率が等しいので△A’BEと△DCA’の『相似比は40㎝：120㎝＝1：3』だと分かります。

BEの長さをＸ、BA’の長さをＹと仮定した場合、それぞれの長さは次のようにあらわすことができます。

BE＝Ｘ
BA’＝Ｙ
A’C＝3Ｘ
CD＝3Ｙ

BA’+A’C＝120なので、次の式が成り立ちます。

BA’+A’C＝120
Ｙ+3Ｘ＝120・・・①

また、AB＝CDなので次の式も成り立ちます。

BE+40＝CD
Ｘ+40＝3Ｙ・・・②

式①②を整理して連立方程式を解くと求めたいBA’であるＹの値が求まります。

3Ｘ+Ｙ＝120・・・①
Ｘ＝3Ｙ-40・・・②

式②を①に代入し、Ｙの値を求めます。

3(3Ｙ-40)+Ｙ＝120
9Ｙ-120+Ｙ＝120
10Ｙ＝240
Ｙ＝24㎝

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。