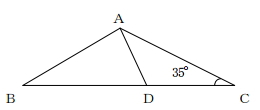
(5)下図の三角形ABCで、点Dは辺BC上にあり、BA=BD、DA=DC、∠ACD=35°である。このとき、∠ABDの大きさを求めなさい。
解答と解説
試験問題の解答:40°
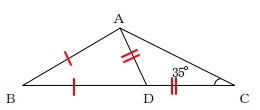
DA=DCなので、三角形ADCは二等辺三角形になります。よって、∠DACも35°になります。
∠DAC=35°
このことより、三角形ADCの残り1角の∠ADCの角度は、次の通り。
∠ADC=180-35-35=110°
∠ADCが110°と分かったので、∠ADBも求まります。
∠ADB=180-110=70°
また、設問よりBA=BDなので三角形ABDもまた二等辺三角形。よって、∠ADB=∠DABとなります。
∠DAB=∠ADB=70°
三角形ADBの3角の内、2角が分かったので残る∠ABDの角度も求まります。
∠ABD=180-70-70=40°
よって、求める∠ABDは、40° となります。

