東京 職業訓練 試験問題[学力検査] 数学-問4(平成30年4月生)

問４ 試験問題

大小2つの自然数があります。その差は2で、積は195です。大きい方の自然数を答えなさい。

解答と解説

試験問題４の解答：15

まず、この問題を解くに当たり自然数が何なのかについて知っている必要があります。

自然数とは『正の整数』で『1、2、3、・・・』という数字を表します。『自然界のものを数えるときに使う数字』と覚えておけば良いかと思います。

自然界にある木や動物を数える場合、『1、2、3・・・』と数え『1.1、1.2、1.3』のように小数や『1/2、1/3、1/4』といった分数で数えることはありませんよね。注意点としては『0』は自然数ではないという点です。自然界のものを数えるときに0から数えることは通常ありません。

さて、本題に戻りたいと思います。

求めたい大きい方の自然数をＮと仮定した場合、小さい方の自然数は大きい方の自然数よりも2小さいので次のように表すことができます。

大きい方の自然数＝Ｎ
小さい方の自然数＝Ｎ-2

また、この2つの自然数の積(掛け算)が195になるとのことなので、次の式が成り立ちます。

Ｎ×(Ｎ-2)＝195

この式を解くと求めたい大きい方の自然数Ｎが求まります。

Ｎ×(Ｎ-2)＝195
Ｎ²-2Ｎ-195＝0
(Ｎ-15)(Ｎ+13)＝0

よって、Ｎ＝15、-13

問題文よりＮは自然数なので-13は対象外となります。

よって、求めたい大きい方の自然数は15

因数分解の補足解説

『Ｎ²-2Ｎ-195＝0』を簡単に因数分解できるよという人はこの補足解説を読む必要はありません。

『Ｎ²+ａＮ+ｂ＝0』を因数分解する場合、足して『ａ』、掛けて『ｂ』になる数値を探さないとダメなのですが、ｂの数が大きくなればなるほど見つけるのが困難になります。今回の場合であれば足して『-2』、掛けて『-195』になる数値を探すのですが、なかなか見つかりませんよね。

せいぜい、簡単にみつけられるのは下表の内容くらいではないでしょうか？

しかし、いずれにも該当しません。

そこで、素因数分解を利用します。195を素因数分解すると次のようになります。

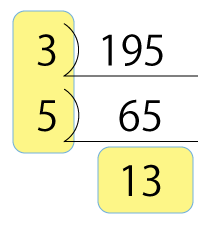
195=3×5×13

ここで『3,5,13』の3つの数字が出てきました。この3つの数字は素因数分解した数値なので195を割れる数だとすぐに分かりますが、その他の195を割れる数字(約数)もこの3つの数字の掛け合わせからすべて求めることができます。

掛けて-195になる数値を下表にまとめなおしてみました。

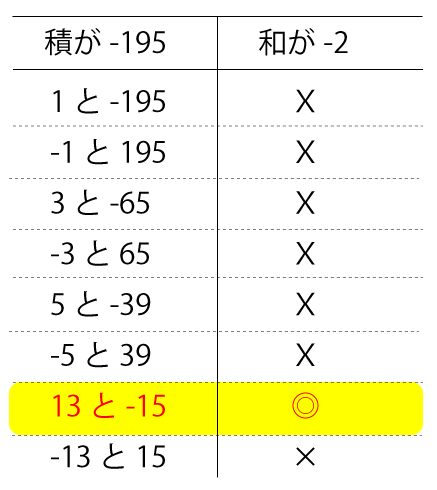
これで掛けて-195、足して-2になる組み合わせが『13、-15』だと分かりました。

よって、『Ｎ²-2Ｎ-195＝0』を因数分解すると『(Ｎ-15)(Ｎ+13)＝0』と導くことができます。

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。