次の図で、立体Ａ－ＢＣＤＥは正四角すいである。底面 ＢＣＤＥは一辺の長さが6cmの正方形であり、ＡＢ＝8cmである。Ｆは底面 ＢＣＤＥの対角線の交点である。このとき、直線ＡＦは底面ＢＣＤＥと垂直である。Ｇは、Ｂから辺ＡＣにひいた垂線と辺ＡＣとの交点である。Ｈは、辺ＡＤ上にあってＤＨ＝2ＣＧ となる点で、ＢとＨを結ぶ。次の各問の答えとして正しいものをア～オの中から1つ選び、記号で答えなさい。

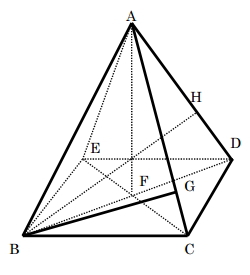
h27-2-20-q4-1

[問題１] 正四角すいＡ－ＢＣＤＥの体積を求めなさい。

[解答群]
ア　18√46
イ　36√46
ウ　12√46
エ　18√58
オ　12√58

[問題２] 線分ＣＧの長さを求めなさい。

[解答群]
ア　1
イ　3/2
ウ　9/4
エ　1/3
オ　7/9

[問題３] △ＡＦＤ∽△ＢＨＤである。相似比を求めなさい。

[解答群]
ア　4：3√2
イ　4：√2
ウ　4：3
エ　4：2
オ　√2：3

解答と解説

問題１の解説：
この問題を解くには、四角錐の体積を求める公式、三平方の定理、三角比を知っておく必要があります。

◎四角すいの体積
　四角すいの体積＝底面積 × 高さ ÷ 3

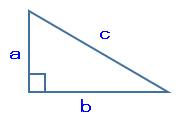
◎三平方の定理
三平方の定理

上図のような直角三角形がある場合、各辺の長さは次の式の関係が成り立ちます。

　ｃ²＝ａ²＋ｂ²

◎三角比
直角二等辺三角形の各辺の比は、下図の通り1：1：√2となる。
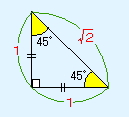
tokyo-sugaku-h25-01-q2-3

さて、上の公式や定理を頭に入れて問題を解いていきます。

底面積は、四角形ＢＣＤＥの面積になります。正四角すいということは、この四角形ＢＣＤＥは正方形。1辺の長さが6cmなので、底面積である四角形ＢＣＤＥの面積は次の通り。

　底面積＝6×6＝36cm²

あとは、高さＡＦが求まれば体積を求めることができるので、ＡＦを求めます。まずは、底面の正方形ＢＣＤＥについて見ていきます。下図の様に三角形ＥＦＢは、直角二等辺三角形。

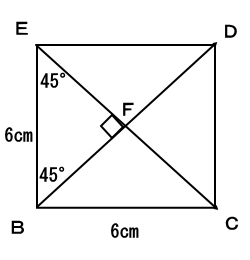
h27-2-20-q4-2

よって、三角比を使うことができます。

　ＦＥ：ＦＢ：ＥＢ＝1：1：√2

が成り立つことになります。よって、ＦＥ、ＦＢの長さは、ＥＢの長さの1/√2になるはずなので、ＥＢの長さが6cmということは、ＦＥ、ＦＢの長さは、

　ＦＥ＝ＦＢ＝6×1/√2
　　　　　　＝6/√2

となります。次に三角形ＡＢＦについて見ていきます。下図の様に三角形ＡＢＦも直角三角形です。

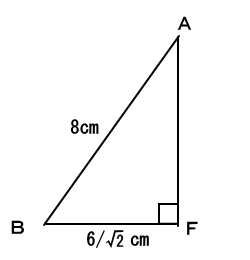
h27-2-20-q4-3

辺ＢＦは先程長さがわかったので、三平方の定理を使用することができます。

　ＡＢ²＝ＡＦ²＋ＢＦ²
　8²＝ＡＦ²＋(6/√2)²
　64＝ＡＦ²＋36/2
　64＝ＡＦ²＋18
　ＡＦ²＝46
　ＡＦ＝√46

ＡＦの高さが分かりました。よって、三角錐の体積は次の通り。

　三角錐の体積＝底面積×高さ÷3
　　　　　　　＝36×√46÷3
　　　　　　　＝12√46

解答：ウ

問題２の解説：
まずは、三角形ＡＢＣを見てください。下図のように頂点Ａから辺ＢＣへ垂直に下ろし辺ＢＣとの交点をＫとします。そうすると、辺ＢＣの長さは6cmなので線分ＢＫは3cmだとわかります。

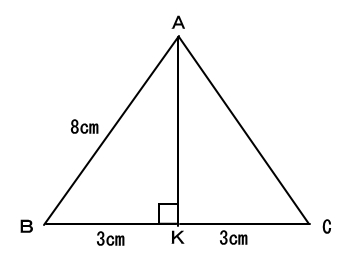
h27-2-20-q4-4

次に三角形ＡＢＫと三角形ＢＣＧについて見てください。∠ＡＢＫと∠ＢＣＧは同じ角度です。更に∠ＡＫＢと∠ＢＧＣはともに90°です。2つの角度が同じということは、この二つの三角形は相似な三角形ということになります。

三角形ＢＣＧが横向いているので分かりやすく立てると下図のようになります。

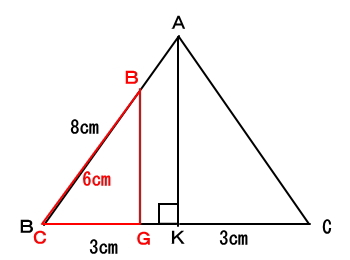
h27-2-20-q4-5

よって、辺ＡＢと辺ＢＣの長さの比が

　ＡＢ：ＢＣ＝8：6

だと分かります。要は、辺ＢＣは、辺ＡＢの6/8の長さですね。相似な三角形の場合、その他の辺の長さ比も同じになるので、辺ＢＫ＝3cmということは、辺ＣＧの長さは、辺ＢＫの6/8なので、

　辺ＣＧ＝3 × 6/8
　　　　＝18/8
　　　　＝9/4

解答：ウ

問題３の解説：
問２と考え方は同じですね。

　ＤＨ＝2ＣＧ

なので、問題２よりＣＧ＝9/4と分かっています。よって、ＤＨの長さは、

　ＤＨ＝2×(9/4)＝9/2

三角形ＢＨＤの辺ＤＨに相当するのが、三角形ＡＦＤの辺ＦＤになります。辺ＦＤの長さは、辺ＦＢと同じです。辺ＦＢの長さは、問題１の中で6/√2だと分かっています。

よって、△ＡＦＤと△ＢＨＤの相似比は

　△ＡＦＤ：△ＢＨＤ＝6/√2：9/2

分数比を整数比にするために2√2を掛けます。

　△ＡＦＤ：△ＢＨＤ＝6/√2×2√2：9/2 × 2√2
　　　　　　　　　　＝12：9√2
　　　　　　　　　　＝4：3√2

解答：ア

※解説の内容が分からない場合はコメント下さい。